Кодирование целых положительных чисел.
Кодирование -- преобразование состояния Система кодирования -- правила кодового обозначения объектов, используемые для удобной и эффективной обработки информации. Вся информация (данные и команды) представлена в виде двоичных кодов. Ячейка памяти ОЗУ, к которой можно обратиться, имеет длину 1 байт. Каждый байт ОЗУ имеет свой адрес. Поле -- последовательность битов в определенном формате, имеющая некоторый смысл. Машинное слово -- наибольшая последовательность разрядов (бит), которую ЭВМ может обрабатывать как единое целое. Его длина зависит от разрядности процессора (16, 32, 64 бита). Различают слово, полуслово, двойное слово. Если длина машинного слова 16 бит, то наибольшее целое число, которое может быть в них записано равно Сложение и умножение производятся по правилам:
Кодирование целых чисел со знаком. Прямой код двоичного числа включает в себя код знака (знак
Вертикальная линия отделяет знаковый разряд от абсолютного значения числа. Обратный код положительных чисел такой же как и прямой код, в знаковом разряде -- 0. Для получения обратного кода отрицательного числа его разряды инвертируются (0 заменяется на 1 и наоборот), в знаковом разряде -- цифра 1:
Дополнительный код положительных чисел такой же как и прямой код. У отрицательных чисел дополнительный код равен результату суммирования обратного кода числа с единицей младшего разряда:
В ЭВМ разность К этому же результату можно прийти иначе: сместим положение нуля на середину интервала 0 - 65535 и будем считать, что числа из первой половины 0-32767 положительные, а числа из второй половины 32769 - 65535 отрицательные. Тогда Пример. Рассмотрим операции 6+7=13, 14-8=6, 5*3=15, 12:4=3 в двоичных числах. Например, в десятичной системе: 5-3=2. Дополнительный код для 3 равен 7 (3+7=10). Так как 5+7=12, то отбрасывая старший разряд получаем 2. Тот же пример в двоичной системе: 0101-0011=0010; дополнительный код для 0011 равен 1101 (0011+1101=1 0000). Итак 0101+1101=10010. Старший разряд отбрасывается, получается Кодирование действительных чисел. Так как в ЭВМ для записи числа отводится конечное число разрядов, то количество возможных значений записываемых чисел конечно, например: 0.0000; 0.0001; 0.0002;...; 0.3960; 0.3961; 0.3962;... Действительные числа образуют континуум -- непрерывное множество. Машинные числа приближенно соответствуют отображаемым числам: числа 0.0000145 и 0.396131 будут восприниматься ЭВМ как 0.0000 и 0.3961, то есть приближенно. Это приводит к следующему: 1. Строгие соотношения между действительными числами 2. Так как отображения действительных чисел являются приближенными, то математическая обработка действительных чисел в ЭВМ ведется с погрешностью. 3. Математическое понятие нуля заменяется понятием "машинный нуль", как значения, которое меньше некоторой определенной величины. Число называется нормализованным в системе счисления Пример. Представление чисел в нормализованном виде: Мантисса двоичного числа лежит в интервале
Числа типа Real на языке Pascal размещаются 6 байтах, числа типа Extended занимают 10 байт. Кодирование двоично-десятичных чисел. Для вывода чисел на экран используется двоично-десятичное представление чисел. В упакованном формате для каждой десятичной цифры отводится по 4 двоичных разряда (полбайта), при этом знак числа кодируется в крайнем правом полубайте числа (1100 -- знак При выполнении сложения и вычитания двоично-десятичных чисел используется упакованный формат: В распакованном формате для каждой десятичной цифры отводится по целому байту, при этом старшие полубайты (зона) каждого байта (кроме самого младшего) в ЭВМ заполняются кодом 0011, а в младших (левых) полубайтах обычным образом кодируются десятичные цифры. Старший полубайт (зона) самого младшего (правого) байта используется для кодирования знака числа. Структура поля упакованного формата:
Распакованный формат используется при вводе - выводе информации, а также при выполнении операций умножения и деления двоично-десятичных чисел. Пример. Число а) в упакованном формате: б) в распакованном формате:
|

 системы в сообщение
системы в сообщение  посредством некоторого оператора
посредством некоторого оператора  :
:  , где
, где 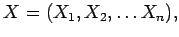
 -- конечные множества состояний системы и соответствующих им сообщений (знаков в алфавите).
-- конечные множества состояний системы и соответствующих им сообщений (знаков в алфавите). , а наименьшее -- 0. В языке Pascal такие числа определены как Word. Числа типа Longint занимают в памяти ЭВМ 4 байта.
, а наименьшее -- 0. В языке Pascal такие числа определены как Word. Числа типа Longint занимают в памяти ЭВМ 4 байта.
 соответствует 0, знак
соответствует 0, знак  - 1) и абсолютное значение этого числа:
- 1) и абсолютное значение этого числа:


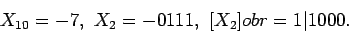


 находится так: оба числа переводятся в дополнительный код, затем складываются и единица в самом старшем разряде отбрасывается. То есть вычитание сводится к сложению, осуществляемому с помощью сумматора.
находится так: оба числа переводятся в дополнительный код, затем складываются и единица в самом старшем разряде отбрасывается. То есть вычитание сводится к сложению, осуществляемому с помощью сумматора. -- код отрицательного числа, а
-- код отрицательного числа, а 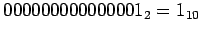 -- код положительного числа. Это соответствует типу Integer на языке Pascal, при размещении чисел из интервала [-32768;32767] в 2 байтном машинном слове.
-- код положительного числа. Это соответствует типу Integer на языке Pascal, при размещении чисел из интервала [-32768;32767] в 2 байтном машинном слове. .
. оказываются нестрогими для их отображений
оказываются нестрогими для их отображений  то
то  .
. , если оно представлено в виде
, если оно представлено в виде  где
где  -- мантисса, лежащая в интервале
-- мантисса, лежащая в интервале 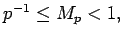
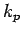 -- порядок числа.
-- порядок числа. в форме чисел с фиксированной запятой:
в форме чисел с фиксированной запятой: 
 , то есть содержит только цифры дробной части, которая всегда начинается на 1. Поэтому ноль в разряде целых, запятую, отделяющую дробную часть, и первую цифру дробной части мантиссы можно не сохранять, но восстанавливать при вычислениях. Пример размещения числа
, то есть содержит только цифры дробной части, которая всегда начинается на 1. Поэтому ноль в разряде целых, запятую, отделяющую дробную часть, и первую цифру дробной части мантиссы можно не сохранять, но восстанавливать при вычислениях. Пример размещения числа  в 32 разрядах:
в 32 разрядах:
 Цифра
Цифра  Цифра
Цифра 
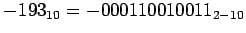 имеет следующий вид:
имеет следующий вид: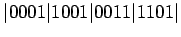 ,
, .
.


