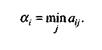Оценки игры
Рассмотрим матричную игру, представленную матрицей выигрышей m×n, где число строк i = Подход игрока 1. Он должен получить максимальный гарантированный результат при наихудших условиях. Значит, при выборе своей чистой стратегии, отвечающей этим условиям, он должен выбрать гарантированный результат в наихудших условиях, т.е. наименьшее значение своего выигрыша aij, которое обозначим
Чтобы этот гарантированный результат в наихудших условиях был максимальным, нужно из всех а, выбрать наибольшее значение. Обозначим его а и назовем чистой нижней ценой игры (максимин):
Таким образом, максиминной стратегии отвечает строка матицы, которой соответствует элемент α. Какие бы стратегии ни применял игрок 2, игрок 1 максиминной чистой стратегией гарантировал себе выигрыш, не меньший чем α;. Таково оптимальное поведение игрока 1. Подход игрока 2. Своими оптимальными стратегиями он стремится уменьшить выигрыш игрока 1, поэтому при каждой j-й чистой стратегии он отыскивает величину своего максимального проигрыша:
в каждом j -м столбце, т.е. определяет максимальный выигрыш игрока 1, если игрок 2 применит j -ю чистую стратегию. Из всех своих nj -х чистых стратегий он отыскивает такую, при которой игрок 1 получит минимальный выигрыш, т.е. определяет чистую верхнюю цену игры (минимакс): Чистая верхняя цена игры показывает, какой максимальный выигрыш может гарантировать игрок 1, применяя свои чистые стратегии, – выигрыш, не меньший, чем α. Игрок 2 за счет указанного выше выбора своих чистых стратегий не допустит, чтобы игрок 1 мог получить выигрыш, больший, чем β. Таким образом, минимаксная стратегия отображается столбцом платежной матрицы, в котором находится элемент β; (см. табл. 4.1). Это оптимальная чистая гарантирующая стратегия игрока 2, если он ничего не знает о действиях игрока 1. Чистая цена игры – цена данной игры, если нижняя и верхняя ее цены совпадают:
В этом случае игра называется игрой с седловой точкой.
|

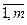 , а число столбцов j =
, а число столбцов j =  (см. табл. 4.1). Применим принцип получения максимального гарантированного результата при наихудших условиях. Игрок 1 стремится принять такую стратегию, которая должна обеспечить максимальный проигрыш игрока 2. Соответственно игрок 2 стремится принять стратегию, обеспечивающую минимальный выигрыш игрока 1. Рассмотрим оба этих подхода.
(см. табл. 4.1). Применим принцип получения максимального гарантированного результата при наихудших условиях. Игрок 1 стремится принять такую стратегию, которая должна обеспечить максимальный проигрыш игрока 2. Соответственно игрок 2 стремится принять стратегию, обеспечивающую минимальный выигрыш игрока 1. Рассмотрим оба этих подхода.