Неопределенность и риск в управленческих решениях

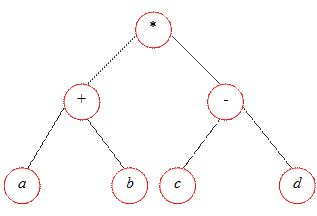
Створимо бінарне дерево із заданою користувачем кількістю вузлів. Тип вузла (компонента) дерева було оголошено у розділі 10.3.1. Оскільки структура дерева визначена рекурсивно, то для його створення та відображення можна розробити рекурсивні підпрограми.

Функція створення дерева tree отримує один цілочисловий параметр Amount-Node, що визначає кількість вузлів дерва та повертає покажчик на його корінь. Якщо кількість вузлів дорівнює нулю, дерево порожнє, а отже, виконано умову завершення рекурсії і функція має повернути значенняnil. Якщо кількість вузлів дерева відрізняється від нуля, необхідно виділити пам’ять для кореня дерева, за наведеними вище формулами обчислити кількість вузлів у лівому та правому піддеревах і двічі рекурсивно викликати функцію tree для створення піддерев. Для посилання на корінь дерева використаємо локальний покажчик newnode. Значення покажчиків на корені піддерев, що їх повертатиме функція tree в результаті рекурсивних викликів, слід присвоїти полям left та right змінної newnode^.

Дерево відображатиме рекурсивна процедура printtree. Піддерево рівня L виводитимиться так: спочатку буде відображене ліве піддерево, ротім – корінь піддерева рівня L,перед яким буде виведено L пробілів, далі – праве піддерево. Приклад створюваного програмою ех10_6 дерева зображено на рис. 10.16 і 10.17. Дерева такого типу називаються синтаксичним деревами арифметичних виразів.

program ex10_6; {створення та відобрвження бінарного дерева}

type ptr=^node; {тип покажчика на вузол дерева }

node=record {тип вузла дерева }

data:string; {інформаційне поле вузла }

left, {показчик на ліве піддерево }

right:ptr; {покажчик на праве піддерево }

end;

var n:integer; {кількість вузлів дерева }

root:ptr; {покажчик на корінь дерева }

{============== створення бінарного дерева =============}

function Tree(AmountNode:integer):ptr;

{AmountNode - kilkist vyzliv dereva,

ptr - pokazhchuk na korin dereva}

var newnode:ptr; {покажчик на новий вузол }

LeftNodes, {кількість вузлів у лівому}

RightNodes:integer; {і правому піддеревах }

str:string; {інформаційне поле вузла }

begin

if AmountNode =0 then {якщо вузлів не має }

tree:=nil {дерево порожнє }

else

begin

LeftNodes:= AmountNode div 2; {кількість вузлів у піддеравах}

RightNodes:= AmountNode - LeftNodes -1;

write('Enter node data:');

readln(str);

New(newnode); {виділити пам’ять для нового вузла}

with newnode^ do

begin

data:=str; {задати інформаційне поле вузла }

{створити ліве піддерево }

left:=Tree(LeftNodes);

right:=Tree(rightNodes);

end;

Tree:=newnode; {значення, що повертається }

end;

end;

{================== відображення дерева ===========}

procedure Printtree(RootTree:ptr;L:integer);

{RootTree - pokazchik na korin dereva; L – номер рівня

var i:integer; {параметр циклу }

begin

if RootTree<>nil then {дерево не порожнє}

with RootTree^ do

begin

Printtree(left,l+1); {вивести ліве піддерево}

for i:=1 to l do write(' ');

writeln(data); {вивести значення вузла}

Printtree(right,l+1); {вивести праве піддерево}

end;

end;

{================ основна програма =====================}

begin

writeln('Create and display tree');

writeln('Enter number of tree''s nodes');

readln(n); {задати кількість вузлів дерева }

root:=Tree(n); {створити дерево }

writeln('Created tree');

Printtree(root,0); {відобразити дерево }

readln;

end.

 

Неопределенность и риск в управленческих решениях

 

Как уже отмечалось, решения могут приниматься в условиях опре­деленности, неопределенности, риска и конфликта (иногда условия конфликта приравниваются к условиям неопределенности). Вопросы принятия решений в условиях определенности были рассмотрены выше. Рассмотрим основные аспекты принятия управленческих решений в условиях неопределенности и риска.