В методе предельных состояний
Прочностные характеристики бетона и арматуры, как и большинства материалов, не являются постоянными величинами в пределах назначенных классов. Так, например, прочность бетона, изготовленного из одной исходной смеси, может изменяться в значительных пределах в зависимости от целого ряда технологических факторов, размера и формы изделия, условий и сроков твердения, характера приложения и длительности действия нагрузки. Для того, чтобы обеспечить требуемую надежность конструкции, необходимо для бетона или арматурной стали данного класса назначить такие величины расчетных сопротивлений, которые в подавляющем большинстве случаев были бы не ниже возможных фактических сопротивлений бетона и арматуры в конструкции. Как следует из опытных наблюдений, изменчивость прочностных характеристик бетона и арматуры имеет случайный характер и подчиняется вероятностно-статистическим законам. Поэтому для оценки прочностных характеристик бетона и арматуры, внесенных в методы расчета железобетонных конструкций используют вероятностный подход. Изменчивость прочности бетона и арматуры принято характеризовать так называемыми кривыми распределения прочности, представляющими собой график, но оси абсцисс которого откладывают прочностную характеристику (бетона или арматуры), получаемую из испытаний большого количества образцов одного класса по прочности, а на оси ординат – частоту (количество) случаев появления того или иного значения прочностной характеристики (рис. 6.8а).
Рис. 6.8. Гистограмма опытных результатов при испытании прочности бетона (а), кривые нормального распределения прочностей материала (б, в) и зависимость «p–t» (г) Такие кривые (см. рис. 6.8б) принято называть кривыми нормального распределения. В качестве теоретической функции распределения случайной величины принята функция нормального распределения Гаусса. Из графика нормального распределения, показанного на рис. 6.8в, следует, что средняя прочность fm соответствует пику этой кривой, т.е. наибольшей частоте случаев. Остальные значения отклоняются от среднего в ту либо иную сторону. Причем, чем больше отклонение, тем реже оно наблюдается в испытаниях. Таким образом, для использования в расчетах следует назначать такое сопротивление материала, выраженное через отклонение от средней прочности, частота появления которого была бы заранее задана:
где t – статистика распределения или число, характеризующее площадь, ограниченную осью абсцисс и кривой распределения. Отношение Для определения нормативных прочностных характеристик материалов принимают значение обеспеченности не менее 0,95, обозначающее, что не менее чем в 95 случаях из 100 прочность материала будет выше нормативной. Такая обеспеченность является весьма высокой и дает ощутимый запас прочности конструкции. Тогда связь между нормативным и средним значениями прочности при t = 1,64 (см. рис. 6.8г) выражается формулой: где fk – нормативное значение прочности; fm – средняя прочность; Vx – коэффициент вариации прочности, принимаемый по результатам статистических оценок. Вопросы для самоконтроля 1. Что понимается под предельным состоянием конструктивной системы или ее элемента? 2. Какие выделены группы предельных состояний и какие расчеты конструкций они включают? 3. На какие виды и группы воздействий рассчитываются железобетонные конструкции в методе предельных состояний? 4. Что представляет собой система частных коэффициентов безопасности в методе расчета железобетонных конструкций по предельным состояниям? 5. Как устанавливаются нормативные и расчетные сопротивления бетона и арматуры с учетом вероятностного подхода оценки изменчивости их прочностных характеристик? 6. В чем заключается расчет прочности железобетонных конструкций по 1-й группе предельных состояний? 7. В чем заключается расчет трещиностойкости и по деформациям железобетонных конструкций во 2-й группе предельных состояний?
вопросы к Тестовому контролю 1. В чем состоит сущность железобетона и почему высокопрочную арматуру нельзя использовать без предварительного напряжения? 2. Что представляет собой структура бетона? 3. Какие формы образцов бетона применяют для испытания его прочности при сжатии и растяжении? 4. Что означает гарантированная прочность бетона? С какой обеспеченностью она назначается? 5. Что такое «класс бетона по прочности на сжатие»? 6. Что такое марка бетона? 7. Какие параметрические точки диаграммы « 8. Какие факторы вызывают проявления объемных деформаций бетона? 9. Из каких слагаемых состоит полная деформация бетона при однократном кратковременном нагружении? 10. Что какое «модуль продольных деформаций» бетона, и какова его геометрическая интерпретация? 11. Как подразделяется арматура по своему назначению и технологии изготовления? 12. Какие параметрические точки диаграммы « 13. Как изобразить диаграмму растяжения различных арматурных сталей? 14. Что такое физический предел текучести и условный предел текучести стали? 15. Каковы условия совместной работы и факторы, обеспечивающие прочность сцепления арматуры и бетона? 16. От чего зависит длина анкеровки арматурных стержней в бетоне? 17. Как отражается усадка и ползучесть бетона на работе железобетонных конструкций? 18. В чем назначение защитного слоя бетона в конструкциях и как определяется его толщина? 19. Как протекает и чем заканчивается 1-я стадия напряженно-деформированного состояния нормального сечения железобетонной балки в зоне чистого изгиба? 20. Как развивается процесс образования и раскрытия трещин во 2-й стадии напряженно-деформированного состояния нормального сечения железобетонной балки в зоне чистого изгиба? 21. Объясните физическую сущность случаев разрушения по нормальному сечению в 3-й стадии напряженно-деформированного состояния нормального сечения железобетонной балки в зоне чистого изгиба? 22. Что понимается под предельным состоянием конструктивной системы или ее элемента? 23. Какие выделены группы предельных состояний и какие расчеты конструкций они включают? 24. Как устанавливаются нормативные и расчетные сопротивления бетона и арматуры с учетом вероятностного подхода оценки изменчивости их прочностных характеристик? 25. В чем заключается расчет прочности железобетонных конструкций по 1-й группе предельных состояний? 26. В чем заключается расчет трещиностойкости и по деформациям железобетонных конструкций во 2-й группе предельных состояний?
Раздел 2. Расчеты железобетонных конструкций по предельным состояниям
|



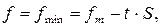 (7.9)
(7.9)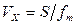 называется коэффициентом изменчивости или коэффициентом вариации. Таким образом, несложно заметить, что кривые распределения, имея одинаковую среднюю прочность fm, могут отличаться по своей форме (рис. 6.8б), которая характеризуется коэффициентом вариации Vx.
называется коэффициентом изменчивости или коэффициентом вариации. Таким образом, несложно заметить, что кривые распределения, имея одинаковую среднюю прочность fm, могут отличаться по своей форме (рис. 6.8б), которая характеризуется коэффициентом вариации Vx.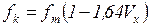 (7.10)
(7.10) » регламентируются нормами проектирования?
» регламентируются нормами проектирования? » при растяжении регламентируются нормами проектирования?
» при растяжении регламентируются нормами проектирования?


