ПОДГОТОВКА ИНФОРМАЦИИ ДЛЯ ПРОВЕДЕНИЯ КРАТКОСРОЧНОГО УПРАВЛЕНЧЕСКОГО АНАЛИЗА
Важнейшая задача подготовки информации для целей проведения краткосрочного управленческого анализа состоит в разделении всех расходов организации на постоянные и переменные. Основной проблемой здесь является разделение совокупных затрат на постоянную и переменную части и приведение их к виду функции у = а + вх, где у – совокупные затраты за месяц, а – постоянная часть затрат, в – переменная часть затрат, х – объем реализованной продукции в физическом выражении за соответствующий месяц. Рассмотрим 2 способа выделения переменной части затрат из общей их суммы. Метод высшей и низшей точек. Расчеты необходимо производить в следующем порядке: 1. Определить месяцы с наибольшим (хmax) и наименьшим (хmin) объемом продаж продукции, а также величину совокупных затрат за эти месяцы – уmax и уmin. 2. Найти отклонения объема продаж (
3. Вычислить ставку переменных расходов на единицу реализованной продукции (bед):
4. Рассчитать общую сумму переменных расходов в максимальной (bmax) и минимальной (bmin) точках:
5. Найти постоянную часть расходов (а) как разность между общими расходами и переменной их частью. Расчет рекомендуется проделать и для минимальной, и для максимальной точек, чтобы убедиться в равенстве полученных результатов:
6. Записать полученное уравнение линейной связи с учетом рассчитанных значений постоянной и переменной частей затрат:
Метод анализа линейной регрессии (наименьших квадратов). Данный метод используется для уточнения результатов, полученных предыдущим способом. Анализ линейной регрессии состоит в нахождении такого уравнения, описывающего поведение прямой, при котором сумма квадратов вертикальных отклонений будет наименьшей. Метод наименьших квадратов заключается в нахождении решения двух уравнений, позволяющих найти параметры а и b. Эти уравнения выглядят следующим образом:
где После преобразования уравнения примут вид:
где Таким образом, получаем уравнение линейной зависимости вида (7.7). После нахождения уравнения зависимости затрат от количества проданной продукции необходимо оценить степень соответствия фактических данных с данными теоретическими (рассчитанными по формуле 7.7). Точность соответствия определяется расхождением между фактическими и теоретическими данными, которое может быть получено как:
где уф – фактическая сумма общих затрат за определенный месяц; утеор – сумма общих затрат за тот же месяц, рассчитанная по формуле 7.7. Оценка точности уравнения производится с помощью коэффициента детерминации R2:
Коэффициент детерминации показывает, какая доля значений величины у находится под влиянием включенных в модель факторов. Полученный коэффициент позволяет судить, насколько точно модель описывает поведение общих затрат в соответствии с количеством реализованного товара. Решение задачи методом анализа линейной регрессии является более сложным, но более точным. Параметр а (постоянная часть расходов), найденный этим методом, будет больше аналогичного параметра, полученного методом высшей и низшей точек. Таким образом, второй метод позволяет более точно определить долю слабо контролируемых предприятием затрат и тем самым лучше учитывает фактор неопределенности. Задача 7.1. Предприятие осуществляет производство и реализацию буровых станков. В табл. 7.1 представлена информация о количестве проданных станков и общей сумме расходов предприятия по месяцам. Получить уравнение зависимости расходов предприятия от количества проданных станков. Задачу необходимо решить методом высшей и низшей точек, а также методом анализа линейной регрессии. Сравнить полученные результаты. Промежуточные расчеты представить в табл. 7.2 и 7.3.
Таблица 7.1
|

 ) и затрат (
) и затрат ( ) в максимальной точке от аналогичных показателей в минимальной точке:
) в максимальной точке от аналогичных показателей в минимальной точке: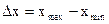 (7.1)
(7.1) (7.2)
(7.2) (7.3)
(7.3) (7.4)
(7.4) (7.5)
(7.5) (7.6)
(7.6) (7.7)
(7.7)
 , (7.8)
, (7.8)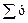 - сумма наблюдений общих затрат; bед – переменные затраты на единицу продукции;
- сумма наблюдений общих затрат; bед – переменные затраты на единицу продукции;  - сумма наблюдений величины продаж; n – количество наблюдений; а – постоянные затраты;
- сумма наблюдений величины продаж; n – количество наблюдений; а – постоянные затраты;  - сумма произведений величины продаж и общих затрат;
- сумма произведений величины продаж и общих затрат;  - сумма наблюдений квадратов величины продаж.
- сумма наблюдений квадратов величины продаж.
 , (7.9)
, (7.9) и
и 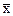 соответственно среднемесячные величины общих затрат и объема реализованной продукции.
соответственно среднемесячные величины общих затрат и объема реализованной продукции. , (7.10)
, (7.10) , % (7.11)
, % (7.11)


