Вибрации в конструкциях РЭС
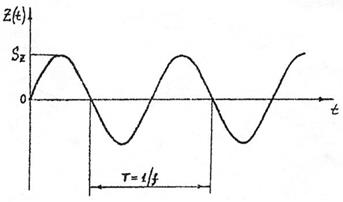
Под вибрацией аппаратуры понимают механические колебания ее элементов или конструкции в целом. Вибрация может быть периодической и случайной. Периодическая вибрация может быть гармонической и полигармонической. Гармоническая вибрация сравнительно редко встречается в реальных условиях, но широко используется при лабораторных испытаниях и при анализе динамических характеристик конструкции и для определения реакции системы при более сложных формах вибрации. Параметрами воздействия вибрации являются частота и ускорение. Гармоническая вибрация описывается законом виброперемещения Z(t), виброскорости
где SZ – амплитуда виброперемещения; w – круговая частота вибрации, 1/с. t – время, с.
Рисунок 8.1 – Виброперемещение при гармонической вибрации Как известно, круговая частота связана с частотой вибрации f(Гц) выражением w = 2pf. По заданному значению виброперемещения при гармонической вибрации легко найти амплитуду виброскорости
Если же задано максимальное значение (амплитуда) виброускорения, то амплитуда гармонической вибрации равна:
Амплитуда виброускорения часто задается в единицах ускорения свободного падения g, (g = 9,81 м/с2). В этом случае амплитуда виброперемещения (в миллиметрах) равна:
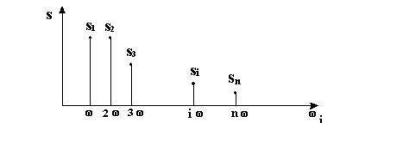
где В реальном случае РЭС подвергается влиянию целого спектра частот вибрации, т.е. вибрация сложная периодическая - полигармоническая.
Рисунок 8.2 – Виброперемещение при гармонической вибрации Из-за ограниченных энергетических возможностей источников вибрации высшие гармоники имеют малую амплитуду. Поэтому, а также из-за трудностей учета всех гармоник, в рассмотрение принимают главным образом низкочастотную часть спектра и, в первую очередь, гармоники с относительно большими амплитудами.
|

 или виброускорения
или виброускорения  .
. 
 ;
; ;
; ,
,
 и виброускорения
и виброускорения  :
: =w2SZ=4p2f2SZ.
=w2SZ=4p2f2SZ.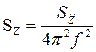 .
. [мм],
[мм],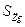 – амплитуда виброускорения в единицах g.
– амплитуда виброускорения в единицах g.