Правило неявного дифференцирования
Рассмотрим пример. Пример 4.5. Пусть функция Вычислить Решение. Продифференцируем обе части уравнения по переменной
Получаем уравнение, которое неявным образом задаёт производную функции
Отсюда находим
Из формулы (4.2) видно, что при неявном дифференцировании производная зависит и от аргумента Вычисляем вторую производную. По определению вторая производная это производная от первой производной (1.5). При неявном дифференцировании для вычисления второй производной необходимо знать уравнение, которому удовлетворяет первая производная. В нашем случае это уравнение (4.1): Применяя правило неявного дифференцирования, получаем Получаем уравнение для вычисления Отсюда находим Замечание. При неявном дифференцировании вторая производная зависит от аргумента Пример 4.6. Найти уравнение касательной и нормальной прямой в точке Решение. Пусть переменная
и
соответственно. Как видно из этих уравнений нам потребуется значение производной функции в точке касания. Применяя правило неявного дифференцирования, вычисляем производную в точке
Отсюда выписываем уравнение для определения производной и вычисляем Подставляя вычисленные значения в уравнение касательной (4.4), получаем
получаем Параметрические задания кривых. Существует ещё один способ задания кривых, при котором координаты считаются равноправными: это задание кривых параметрическими уравнениями. Координаты
Параметр Пример 4.7. Определить уравнения кривых заданных параметрическими уравнениями
Решение. Анализируем первую систему уравнений. Возводим оба уравнения системы 1) в квадрат и, складывая, получаем Если при параметрическом задании функции считать переменную параметрического дифференцирования. Причем производная также записывается в параметрическом виде. Теорема 4.1. Пусть функция Тогда её производная по аргументу
Обозначим для простоты записи в виде Поскольку вторая производная есть производная от первой производной, то применяя правило параметрического дифференцирования к параметрической записи первой производной (4.8) получаем параметрическую запись второй производной
|

 задана неявным образом
задана неявным образом  .
. .
. .
.
 (4.1)
(4.1)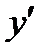
 (4.2)
(4.2) и от значения функции
и от значения функции  .
.

 (4.3)
(4.3) .
. , от функции
, от функции  и её производной
и её производной  .
. к линии заданной уравнением
к линии заданной уравнением  .
.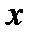 будет аргументом функции
будет аргументом функции  . В данном случае функция
. В данном случае функция  задана неявным образом. Уравнения касательной и нормали в точке касания
задана неявным образом. Уравнения касательной и нормали в точке касания 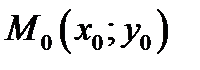 имеют вид
имеют вид (4.4)
(4.4) (4.5)
(4.5)

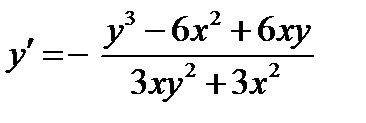 . Поэтому
. Поэтому 
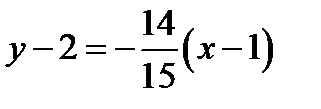 . Подставляя вычисленные значения в уравнение нормали (4.5),
. Подставляя вычисленные значения в уравнение нормали (4.5),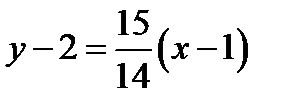 .
.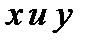
 (скажем, времени)
(скажем, времени) (4.6)
(4.6) .
.
 . Данная кривая это окружность единичного радиуса:
. Данная кривая это окружность единичного радиуса:  . Аналогично для системы 2) получаем
. Аналогично для системы 2) получаем  . Это уравнение прямой линии
. Это уравнение прямой линии  .
. функцией, а переменную
функцией, а переменную  аргументом то возникает вопрос каким образом вычислить производную функции
аргументом то возникает вопрос каким образом вычислить производную функции 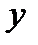
 задана в параметрическом виде
задана в параметрическом виде 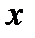
 записывается в параметрическом виде формулами
записывается в параметрическом виде формулами (4.7)
(4.7)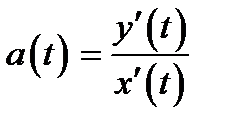 , тогда формулу (4.7) можно переписать
, тогда формулу (4.7) можно переписать (4.8)
(4.8) (4.9)
(4.9)


