Неявное и параметрические задания функций и их дифференцирование.
Глава 4. Занятие 4 Неявное и параметрические задания функций и их дифференцирование. Определение 4.1. Если функция задана формулой, то говорят, что функция задана явным образом. Пусть Например Определение 4.2. Если функция является решением некоторого уравнения, то говорят о неявном задании функции. Вся сложность при неявном задании функции заключается в вычислении значения функции при заданном значении её аргумента. Пример 4.1. Уравнение Пример.4.2. Рассмотрим уравнение
Таким образом, данное уравнение задаёт нам две различных явно заданных функции. Как конкретизировать функцию при её неявном задании. Очень просто нужна дополнительная информация. Пример 4.3. Уравнение Уравнение При неявном задании функции нужно заранее определить какая из двух переменных Например, если считать в уравнении
Если к уравнению получим только одно явное выражение для функции: Пример 4.4. Функция Решение. Решаем квадратное уравнение относительно
Так как Чаще всего невозможно получить явное выражение для функции, которая задана неявно. Однако производную от функции заданной неявно получить несложно из самого уравнения. Такой алгоритм называется правилом неявного дифференцирования.
|

 . Значение такой функции легко вычислить. Нужно заданное значение аргумента подставить в формулу и сосчитать полученное выражение.
. Значение такой функции легко вычислить. Нужно заданное значение аргумента подставить в формулу и сосчитать полученное выражение. .
. определяет функцию
определяет функцию  . В данном случае мы можем решить это уравнение относительно
. В данном случае мы можем решить это уравнение относительно  и получить явное задание
и получить явное задание  .
.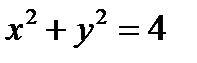 . Оно также задает функцию
. Оно также задает функцию 

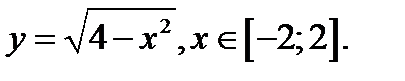

 является аргументом, а какая функцией.
является аргументом, а какая функцией.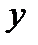 аргументом, а переменную
аргументом, а переменную  функцией, то уравнение задаёт две функции
функцией, то уравнение задаёт две функции
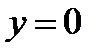 значение
значение  », то
», то .
. задана неявно уравнением
задана неявно уравнением  и дополнительным условием: все значения функции положительные числа.
и дополнительным условием: все значения функции положительные числа.

 , то ответом будет функция
, то ответом будет функция  .
.


