Гибридные автоматы (ГА)
Гибридный автомат определяется как граф системы переходов, в которой каждой вершине ствится в соответствие область пространства состояний системы, характеризующая её непрерывное поведение в промежутках между событиями, приводящими к смене поведения. Этим событиям соответствуют дуги системы переходов. 1.Используются в современных инструментальных средствах визуального моделирования динамических (реактивных) систем. 2.Для гибридного автомата, как и для любой непрерывно-дискретной системы, глобальное поведение описывается последовательностью локальных поведений, смена которых проходит под воздействием событий. 3.Наступление того или иного события зависит от значений непрерывных параметров, а, следовательно, от функций локального поведения. 4.Каждое событие может порождать другие события, а дискретный процесс, результатом которого может быть выбор нового локального поведения, описывается в общем случае нетривиальным алгоритмом. 5.Поведение системы можно представить последовательностью сменяющих друг друга длительных непрерывных и мгновенных дискретных поведений. 6.В математическом плане ГА объединяет язык дифференциальных уравнений и язык конечных автоматов в единый формализм, по своим возможностям весьма напоминающий формализм А-схем.
Примером ГА является система, описываемая в пространстве состояний следующим уравнением:
где У алфавита этого автомата два выходных символа (они же его состояния) Входными сигналами являются сигналы, говорящие о достижении вектором
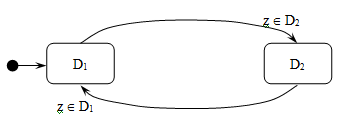
Графическая иллюстрация поведения ГА или карты состояний (statechart) Харела
Состояние
В качестве классического примера системы, описываемой подобным образом, можно привести динамическую систему, исследуемую в теории управления в задаче об успокоении материальной точки с максимальным быстродействием при наличии ограничений на управление (задача о лифте). В формализме ГА, дискретная переменная
|

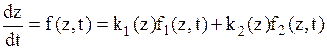 ,
, 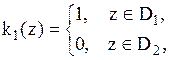
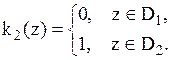
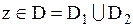 ;
; 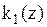 ,
, 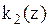 – кусочно-постоянные функции, которые можно представить с помощью конечного автомата.
– кусочно-постоянные функции, которые можно представить с помощью конечного автомата.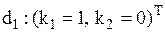 и
и 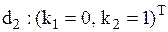 .
.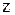 границ областей
границ областей 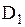 и
и 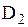 .
.
 .
.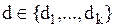 ставится в соответствие множеству
ставится в соответствие множеству 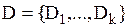 узлов графа, называемых основными состояниями (одно из них помечается как начальное).
узлов графа, называемых основными состояниями (одно из них помечается как начальное).


