События, как правило, происходят группами и по времени почти одновременно.
4.Стационарность – нестационарность Стационарный поток – вероятность появления того или иного количества событий на интервале длительностью
Рассмотрим ординарный поток событий. Среднее число событий за малый интервал времени
Среднее число событий в единицу времени задается как
Если этот предел существует, то его величина называется интенсивностью потока, которая имеет размерность, обратную размерности времени [с-1]. Для стационарного потока интенсивность не зависит от времени Если стационарный поток имеет ограниченное последействие, то при
Плотность распределения первого интервала может быть найдена из соотношения
то есть отличается от плотности в установившемся режиме. Имеет также место соотношение
16. Принципы построения моделирующих алгоритмов для СМО (1,2,3).
Рассмотрим реализацию алгоритма модели системы 1. Задается исходное описание системы – состав элементов и внутренние параметры: 1.1. количество источников входных потоков заявок 1.2. количество фаз обслуживания заявок 1.3. количество накопителей в каждой фазе 1.4. емкости (предельные размеры очереди) накопителей 1.5. количество каналов обслуживания в каждой фазе 2. Задаются связи между элементами типа 3. Задаются дисциплины ожидания заявок в накопителях и их выбора на обслуживание в каналах 4.Если структура и параметры системы заданы, то далее определяется перечень показателей эффективности, которые должны быть оценены в ходе моделирования. Для наглядного представления структуры СМО при разработке алгоритмов и программ используются специальные символические представления,позволяющие существенно упростить процесс создания моделей на языке Q-схем.
Пример изображения структурной схемы СМО В имитационной модели должны присутствовать несколько стандартных элементов, описываемых своими внутренними состояниями.
1. Активные элементы модели типа И–источники заявок. Каждый 2. Пассивные элементы модели типа Н–накопители. Каждый 3. Активно-пассивные элементы модели типа К–каналы обслуживания. Каждый Текущее состояние 4. Очередь заявок (ОЗ) каждой фазы обслуживания. Каждый элемент 5. Очередь каналов (ОК) каждой фазы обслуживания. Каждый элемент Всего будет пять типов стандартных модулей (объектов), состояния которых описываются следующими массивами данных:
17. Современные реализации комбинированного подхода (гибридные автоматы, карты Харела) (1,2,6).
|

 зависит лишь от длины этого интервала и не зависит от того, где на оси времени он расположен
зависит лишь от длины этого интервала и не зависит от того, где на оси времени он расположен ,
, 
 у него равно
у него равно .
. .
. .
. для законов распределения интервалов
для законов распределения интервалов  выполняется
выполняется .
. ,
, .
. , формализованной на основе Q-схем.
, формализованной на основе Q-схем. и их интенсивности
и их интенсивности  ,
,  ;
; ;
; ,
,  ;
; ,
, 
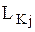
 ,
,  ,
,  ,
,  ,
,  в виде оператора сопряжения
в виде оператора сопряжения  элементарных приборов обслуживания.
элементарных приборов обслуживания.
 описывается текущим состоянием
описывается текущим состоянием  , где
, где  – время поступления очередной заявки от
– время поступления очередной заявки от  – интенсивность потока от
– интенсивность потока от  описывается текущим состоянием
описывается текущим состоянием  , характеризующим длину очереди. Переход из одного состояния в другое происходит мгновенно и сопровождается увеличением
, характеризующим длину очереди. Переход из одного состояния в другое происходит мгновенно и сопровождается увеличением  на единицу при поступлении заявки на вход или уменьшением
на единицу при поступлении заявки на вход или уменьшением  может быть в одном из двух состояний: «занят» и «свободен». В состоянии «занят» канал является активным, то есть формирует интервал времени обслуживания заявки в соответствии с собственными характеристиками потока обслуживания. В состоянии «свободен» канал является пассивным и ждет поступления извне заявки, под воздействием которой переходит в другое состояние («занят».)
может быть в одном из двух состояний: «занят» и «свободен». В состоянии «занят» канал является активным, то есть формирует интервал времени обслуживания заявки в соответствии с собственными характеристиками потока обслуживания. В состоянии «свободен» канал является пассивным и ждет поступления извне заявки, под воздействием которой переходит в другое состояние («занят».)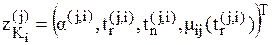 , где
, где  в состоянии «свободен» и
в состоянии «свободен» и  в состоянии «занят»;
в состоянии «занят»;  – время начала обслуживания очередной заявки, а
– время начала обслуживания очередной заявки, а  – время окончания обслуживания очередной заявки (задаются при
– время окончания обслуживания очередной заявки (задаются при  – текущая интенсивность потока обслуживания для момента
– текущая интенсивность потока обслуживания для момента  для
для  -ой фазы является пассивным и его состояние определяется величиной
-ой фазы является пассивным и его состояние определяется величиной  ,
,  . Состояние изменяется мгновенно при поступлении очередной заявки
. Состояние изменяется мгновенно при поступлении очередной заявки 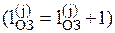 или при освобождении канала фазы
или при освобождении канала фазы  .
. для
для  ,
,  . Состояние меняется мгновенно при поступлении в фазу новой заявки
. Состояние меняется мгновенно при поступлении в фазу новой заявки  или при освобождении какого-либо канала фазы
или при освобождении какого-либо канала фазы  .
. ;
;  ;
; ;
;  ;
;  .
.



