Обработка диаграмм растяжения
Обработку диаграмм растяжения осуществляли в следующей последовательности. Определяли масштаб диаграммы по оси деформаций. Для этого через точку К, соответствующую концу испытания (разрыву образца), проводили прямую
Для определения масштаба диаграммы растяжения по оси нагрузок
Диаграмму растяжения на участке равномерной пластической деформации разбивали на 8 участков. Из точек деления проводили прямые параллельные прямолинейному участку до пересечения с осью деформаций и опускали перпендикуляры на данную ось. Измеряя в миллиметрах длины соответствующих отрезков и используя масштабные коэффициенты, можно получить реальные значения удлинения и нагрузки, соответствующие данному моменту испытаний. На основании полученных значений для каждой точки диаграммы растяжения проводили расчет текущих механических свойств сталей в процессе деформации. Относительное удлинение образца определяется по выражению
в конце равномерного удлинения (точка
Или, выражая в процентах, относительное равномерное удлинение определяется как
В конце испытаний получим относительное удлинение после разрыва
где индекс «100» указывает на начальную расчетную рабочую длину образца. Относительное удлинение в конце испытаний
Относительное сужение поперечного сечения образца
где Учитывая, что в процессе испытаний на растяжение текущий диаметр образца не измеряли, то относительное сужение определялось из закона постоянства объема
В конце равномерного удлинения получим относительное сужение поперечного сече6ния после разрыва
Для исключения влияния масштабного фактора (масштабов по оси деформаций и по оси нагрузок и размеров образца), а также упругой деформации образца и деталей испытательной машины был проведен расчет и построена диаграмма условных напряжений, т.е графическая зависимость условных напряжений
Физический предел текучести Для оценки пластических свойств и сопротивления металла пластической деформации были построены кривые упрочнения первого и второго рода, представляющие графические зависимости сопротивления металла пластической деформации
Данное выражение справедливо только для участка равномерного удлинения. Для момента разрыва образца в соответствии с энергетическим условием пластичности
где Для использования полученных данных в экспериментально-аналитических методах определения напряженно-деформированного состояния при обработке металлов давлением был проведен расчет и построены графические зависимости интенсивности напряжений
|

 параллельную начальному прямолинейному участку диаграммы для исключения упругой деформации деталей испытательной машины и самого образца. Длина отсекаемого отрезка прямой
параллельную начальному прямолинейному участку диаграммы для исключения упругой деформации деталей испытательной машины и самого образца. Длина отсекаемого отрезка прямой  на оси деформаций в миллиметрах в m раз больше остаточного (пластического) удлинения образца после разрыва
на оси деформаций в миллиметрах в m раз больше остаточного (пластического) удлинения образца после разрыва  , мм. Тогда масштаб диаграммы растяжения по оси деформаций равен
, мм. Тогда масштаб диаграммы растяжения по оси деформаций равен .
. необходимо определить положение на диаграмме растяжения точки
необходимо определить положение на диаграмме растяжения точки  , соответствующей максимальной силе растяжения. Для этого на оси деформаций откладывается отрезок численно равный
, соответствующей максимальной силе растяжения. Для этого на оси деформаций откладывается отрезок численно равный  (мм) от начала отсчета точки
(мм) от начала отсчета точки  . Из точки
. Из точки  проводится прямая
проводится прямая  параллельная прямолинейному участку диаграммы до пересечения с ней. Перпендикуляр
параллельная прямолинейному участку диаграммы до пересечения с ней. Перпендикуляр  , опущенный из точки
, опущенный из точки  на ось деформаций (мм) в
на ось деформаций (мм) в  раз меньше зафиксированного численного значения
раз меньше зафиксированного численного значения  , т.е. масштаб по оси нагрузок определяется как
, т.е. масштаб по оси нагрузок определяется как

 ,
,

 рассчитывали по длине
рассчитывали по длине  , определяемой из закона постоянства объема. Тогда
, определяемой из закона постоянства объема. Тогда .
. определяли по формуле
определяли по формуле ,
, - текущая площадь поперечного сечения образца.
- текущая площадь поперечного сечения образца. .
. , %.
, %. от относительного удлинения
от относительного удлинения  :
:  . Величину
. Величину  к начальной площади его поперечного сечения
к начальной площади его поперечного сечения 
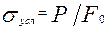 .
. и временное сопротивление (предел прочности)
и временное сопротивление (предел прочности)  , модуль упругости
, модуль упругости  , кроме графического, определяли тензометрическим (расчетным) методом. Диаграмма условных напряжений имеет три характерные точки, соответствующие пределу текучести
, кроме графического, определяли тензометрическим (расчетным) методом. Диаграмма условных напряжений имеет три характерные точки, соответствующие пределу текучести  от относительного удлинения
от относительного удлинения  и
и 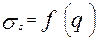 , соответственно. Значения
, соответственно. Значения  .
. ,
, - поправочный коэффициент, зависящий от значения
- поправочный коэффициент, зависящий от значения  .
. от интенсивности деформаций
от интенсивности деформаций  ,
,  . Интенсивность деформаций
. Интенсивность деформаций  в направлении оси образца. Из условия постоянства объема
в направлении оси образца. Из условия постоянства объема




