Постановка задачи и параметры математической модели. Если задача статически определима, т.е
Если задача статически определима, т.е. функция Q(r) известна, то из (7) с учетом (8а), (9а) получаем уравнение типа Ламе
интегрируя которое имеем
Такой же результат получаем, естественно, дифференцируя (2*) с учетом (3*) и (8а). В качестве примера рассмотрим задачу расчета плоского днища цилиндрической оболочки (схема в первом примере граничных условий). Здесь: Подставляя в (8а), (9а) находим
Подставляем в (4а), (5а)
В месте сопряжения с оболочкой
Сравнивая с напряжениями в оболочке, получаем, что напряжения в свободном днище в В заключении определим перемещения. Подставляя полученное выражение для θ в (1*), интегрируя, с учетом граничного условия
Напомним, что расчет проведен в предположении свободного закрепления пластины в направлении радиуса.
Круглые пластины. Моментная теория Постановка задачи и параметры математической модели Задачу удобно решать в цилиндрических координатах, направив ось z по нормали к срединной поверхности, ось r –по радиусу, поместив начало координат в центре пластины. Перемещение по нормали к срединной поверхности –w(r), Гипотеза Бернулли здесь формулируется так: нормаль к срединной поверхности остается прямой. Угол поворота нормали в радиальной плоскости – θ(r). Нагрузка симметрична относительно оси пластины – qz(r)=p(r). Напряжения по нормали к срединной поверхности Примеры – плоское днище цилиндрического сосуда или резервуара, толстая мембрана, цилиндрические упругие элементы, клапана. Параметры задачи: - w(r), перемещение срединной поверхности по оси z; - θ(r), угол поворота нормали в радиальной плоскости; - - Q(r), поперечная сила в радиальной плоскости на единицу длины дуги; - - - - - - В перечне отсутствуют касательные напряжения и поперечные силы в тангенциальной плоскости, так как отсутствуют угловые деформации вследствие симметрии задачи. Касательными напряжениями в радиальной плоскости пренебрегаем как малыми в сравнении с нормальными напряжениями (как и в стержнях). Срединную поверхность считаем не растяжимой. Граничные условия обеспечивают свободу перемещений в радиальном направлении. Все необходимые иллюстрации приведены на рисунке.
|

 ,
, . (5*)
. (5*) ,
, 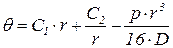 ,
,  ,
,  ,
,  .
. .
.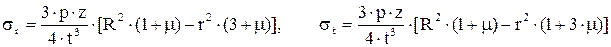 .
. при
при  получаем
получаем .
.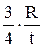 больше. Именно по этому в сосудах используют сферические или полусферические днища.
больше. Именно по этому в сосудах используют сферические или полусферические днища. получаем
получаем .
. малы (порядка давления p) и ими можно пренебречь.
малы (порядка давления p) и ими можно пренебречь. , давление на пластину;
, давление на пластину; , изгибающий момент в радиальной плоскости на единицу длины дуги;
, изгибающий момент в радиальной плоскости на единицу длины дуги; , изгибающий момент в тангенциальной плоскости (касательной к окружности радиусом r) на единицу длины дуги;
, изгибающий момент в тангенциальной плоскости (касательной к окружности радиусом r) на единицу длины дуги; , нормальное напряжение в радиальной плоскости;
, нормальное напряжение в радиальной плоскости; , нормальное напряжение в тангенциальной плоскости;
, нормальное напряжение в тангенциальной плоскости;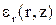 , линейная деформация в радиальной плоскости;
, линейная деформация в радиальной плоскости; , линейная деформация в тангенциальной плоскости.
, линейная деформация в тангенциальной плоскости.


