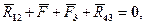Трехшарнирная структурная группа

Расчетная схема для структурной группы с тремя вращательными кинематическими парами представлена на рис. 3.4.

Уравнение равновесия структурной группы в целом в виде равенства нулю суммы всех сил, на нее действующих:

или в проекциях на оси НСК OXoYo:

(3.4)

R_12x + F_2x + F_3x + R_43x = 0;

R_12y + F_2y + F_3y + R_43y = 0.

Равновесие шатуна 2 в виде равенства нулю суммы моментов всех сил относительно точки В:

–R_12x (y_A – y_B) + R_12y (x_A – x_B) – F_2x (y_S2 – y_B) + F_2y (x_S2 – x_B) = 0. (3.5)

Равновесие звена 3 в виде равенства нулю суммы моментов всех сил относительно точки В:

–R_43x (y_С – y_B) + R_43y (x_С – x_B) – F_3x (y_S3 – y_B) + F_3y (x_S3 – x_B) = 0. (3.6)

Уравнения (3.4), (3.5), (3.6) образуют линейную алгебраическую систему относительно неизвестных R_12x, R_12y, R_43x, R_43y, которая легко решается.

Для определения реакции R₂₃ в шарнире В теперь достаточно рассмотреть, равновесие звена 3:

(3.7)

R_23x = – F_3x – R_43x;

R_23y = – F_3y – R_43y.

3.4.2. Структурная группа типа "шатун – ползун";

Расчетная схема для структурной группы данного вида представлена на рис. 3.5. Реакции в направляющих ползуна зависят от его конструкции. Имеется два основных случая:

1. Реакции перемещаются по направляющим вместе с ползуном. В этом случае рабочие длины l ₁, l ₂ являются конструктивными параметрами (см. рис. 3.5,а, 3.5,в).

2. Реакции приложены в неподвижных опорах. В этом случае рабочие длины l ₁, l ₂ необходимо определять в процессе кинематического анализа механизма (см. рис. 3.5,б).

Но в обоих случаях величины l ₁, l ₂ для силового расчета можно считать известными.

В данном случае решение удобно получить в НСК OXY, ось X которой параллельна оси ползуна. Уравнение равновесия структурной группы в целом в виде равенства нулю суммы всех сил, на нее действующих:

или в проекциях на оси НСК OXY:

(3.8)

R_12x + F_2x + F_3x = 0;

R_12y + F_2y + F_3y + R₄₃ ⁽¹⁾ + R₄₃ ⁽²⁾ = 0.

 

Из первого уравнения системы (3.8) сразу определяется составляющая R_12x. Равновесие шатуна 2 в виде равенства нулю суммы моментов всех сил относительно точки В:

 

–R_12x (y _A – y _B) + R_12y (x _A – x _B) – F_2x (y _S2 – y _B) + F_2y (x _S2 – x _B) = 0. (3.9)

 

Отсюда находим R_12y.

Для определения реакций R₄₃⁽¹⁾, R₄₃⁽²⁾ составим систему уравнений, первое из которых отражает равновесие ползуна 3 в виде равенства нулю суммы проекций всех сил на ось Y, а второе – равенство нулю суммы моментов всех сил относительно точки В:

 

(3.10)

F_3y + R₄₃⁽¹⁾ + R₄₃⁽²⁾ = 0;

–R₄₃⁽¹⁾ l ₁ + R₄₃⁽²⁾ l ₂ – F_3x (y _S3 – y _B) + F_3y (x _S3 – x _B) = 0.

 

Длины l ₁, l ₂ надо подставлять с учетом знака, на рис. 3.5 показаны направления, которые считаются положительными.

Для определения реакции R₃₂ в шарнире В достаточно рассмотреть, равновесие шатуна 2 в виде равенства нулю суммы всех сил, на него действующих:

(3.11)

R_32x = – F_2x – R_12x ;

R_32y = – F_2y – R_12y .