Кривошип
Тип силового расчета кривошипа зависит от того, как на него передается крутящий момент с вала двигателя. На рис. 3.12 представлены наиболее распространенные варианты.
Вариант 1. Крутящий момент на кривошип передается через зубчатую или фрикционную пару (рис. 3.12,а). В этом случае крутящий момент, действующий на кривошипе создается усилием в зацеплении и при силовом расчете учитывается так называемой уравновешивающей силой “Fу”, приложение которой уравновешивает кривошип, что и позволяет использовать уравнения равновесия. Плоская расчетная схема для этого варианта представлена на рис. 3.13.
(3.27)
где: h i – плечи, на которых соответствующие силы создают крутящие моменты, на рис. 3.13 показаны плечи h2 и hу . n – количество структурных групп, присоединенных к кривошипу.
Если момент передается через зубчатую пару, то aw (см. рис. 3.13) это угол зацепления, а если через фрикционную – то aw = 0. Если силовой расчет производится после динамического исследования характера движения кривошипа (см. гл. 5), то при вычислении уравновешивающей силы появляется возможность учесть и инерционную нагрузку:
где: MИ = J пр e1 – инерционный момент, действующий на кривошип в данном положении, J пр – значение приведенного момента инерции машины, e1 – значение углового ускорения кривошипа. Реакцию в опоре кривошипа (обозначим ее R01) найдем из условия равновесия в виде равенства нулю суммы всех сил, действующих на кривошип:
Или в проекциях на оси НСК X0Y0:
(3.28)
Характерными особенностями данного варианта являются: 1. Уравновешивающая сила создает дополнительную составляющую реакции в опоре кривошипа.
2. Величина этой дополнительной составляющей зависит от характера внешних сил, диаметра колеса 1 на валу кривошипа и расположения шестерни 2 относительно колеса 1. Вариант 2. Крутящий момент на кривошип передается через планетарный или волновой механизм (рис. 3.12,б). Соответствующая плоская расчетная схема представлена на рис. 3.14. При этом, на рис. 3.14,а – схема с двумя сателлитами как на рис. 3.12,б, а на рис. 3.14,б – с тремя. В этом случае крутящий момент, действующий на кривошип создается несколькими усилиями тоже называемыми уравновешивающими силами, но возникающими в осях сателлитов F у i (i =1, 2,... nw ; где: nw – количество сателлитов). Обычно в силовых механизмах сателлитов не меньше трех. Однако, для силового расчета это не имеет значения, поскольку усилия Fу j в сумме не создают дополнительной реакции в опоре кривошипа т.к.
(3.29)
где: h i – плечи, на которых силы R i создают крутящие моменты, nСГ – количество структурных групп, присоединенных к кривошипу. Слагаемое “MИ” поставлено в скобках т.к. оно учитывается или нет в зависимости от стадии, на которой производится силовой расчет (см. комментарии к уравнениям 3.27). Реакцию в опоре кривошипа R01 находим из условия равновесия в виде равенства нулю суммы всех сил, действующих на кривошип:
(3.30)
Характерной особенностью данного варианта является то, что в опоре кривошипа не возникает дополнительных составляющих реакции, что можно отнести к достоинствам планетарных и волновых механизмов.
|

 Наиболее часто встречающийся случай, когда к кривошипу присоединяется несколько структурных групп – это коленчатый вал, приводящий в движение несколько шатунно-ползунных групп. На рис. 3.11 представлен пример такого механизма с двумя группами. Задача в данном случае состоит в определении реакций в опорах кривошипа.
Наиболее часто встречающийся случай, когда к кривошипу присоединяется несколько структурных групп – это коленчатый вал, приводящий в движение несколько шатунно-ползунных групп. На рис. 3.11 представлен пример такого механизма с двумя группами. Задача в данном случае состоит в определении реакций в опорах кривошипа.
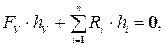
 Уравновешивающая сила определяется из условия равновесия моментов всех сил, действующих на кривошип:
Уравновешивающая сила определяется из условия равновесия моментов всех сил, действующих на кривошип: (3.27,б)
(3.27,б)









