Разбор заданий ЕГЭ
1. Рогожин, М.Ю. Организация делопроизводства предприятия (на основе ГОСТ Р6.30-2003): учебно-практическое пособие / М.Ю. Рогожин. − М.: Издательство РДЛ, 2003. − 208 с. 2. Стенюков, М. В..Делопроизводство: учебное пособие / М.В. Стенюков. − М.: Книга сервис, 2003. − 160 с. 3. Кирсанова, М. В. Курс делопроизводства. Документационное обеспечение управления: учебник / М.В.Кирсанова, Ю.М. Аксенов. − М.: ИНФРА-М; Сибирское соглашение, 2002. − 320 с. 4. Стенюков, М. В. Образцы документов по делопроизводству. Руководство к составлению: учебник / М.В. Стенюков. − М.: Изд-во «ПРИОР», 2001. − 114 с.
Информатика Справочник для подготовки к ЕГЭ-2013
Составитель: Кравцов Михаил,
2012 – 2013 Содержание Разбор заданий ЕГЭ А1 (Системы счисления) – Б1............................................................................................................. 5
А1 (базовый уровень, время – 1 мин) Тема: Системы счисления и двоичное представление информации в памяти компьютера. Что нужно знать: · перевод чисел между десятичной, двоичной, восьмеричной и шестнадцатеричной системами счисления (см. презентацию «Системы счисления»)
· отрицательные целые числа хранятся в памяти в двоичном дополнительном коде · для перевода отрицательного числа (-a) в двоичный дополнительный код нужно сделать следующие операции: o перевести число a-1 в двоичную систему счисления o сделать инверсию битов: заменить все нули на единицы и единицы на нули в пределах разрядной сетки (см. пример далее) Пример задания: Сколько единиц в двоичной записи числа 1025? 1) 1 2) 2 3) 10 4) 11 Решение: 1) переводим число 1025 в двоичную систему: 1025 = 100000000012 2) считаем единицы, их две 3) Ответ: 2
Еще пример задания: Для хранения целого числа со знаком используется один байт. Сколько единиц содержит внутреннее представление числа (-78)? 1) 3 2) 4 3) 5 4) 6 Решение (вариант классический): 1) переводим число 78 в двоичную систему счисления: 78 = 64 + 8 + 4 + 2 = 26 + 23 + 22 + 21 = 10011102 2) по условию число занимает в памяти 1 байт = 8 бит, поэтому нужно представить число с помощью 8 разрядов 3) чтобы получилось всего 8 разрядов (бит), добавляем впереди один ноль: 78 = 010011102 4) делаем инверсию битов (заменяем везде 0 на 1 и 1 на 0): 010011102 → 101100012 5) добавляем к результату единицу 101100012 + 1 = 101100102 это и есть число (-78) в двоичном дополнительно коде 6) в записи этого числа 4 единицы 7) таким образом, верный ответ – 2.
A2 (базовый уровень, время – 2 мин) Тема: Использование информационных моделей (таблицы, диаграммы, графики). Что нужно знать: · в принципе, особых дополнительных знаний, кроме здравого смысла и умения перебирать варианты (не пропустив ни одного!) здесь, как правило, не требуется Пример задания: Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)
Определите длину кратчайшего пути между пунктами A и F (при условии, что передвигаться можно только по построенным дорогам). 1) 9 2) 10 3) 11 4) 12 Решение: 1) составим граф, который показывает, куда (и как) можно ехать из пункта А, рядом с дугами будем записывать увеличение пути, а рядом с названиями пунктов – общую длину пути от пункта A:
2) видно, что напрямую в пункт F из A не доехать 3) строим граф возможных путей дальше: определяем, куда можно ехать из B и C (конечно, не возвращаясь обратно); из B можно ехать только в A (обратно), в C и в E; 4) узел C уже есть на схеме, и оказывается, что короче ехать в него по маршруту A-B-C, чем напрямую A-C, длина «окольного» пути составляет 3 вместо 4 для «прямого»;
5) строим маршруты из пункта C; кроме A и B, из пункта C можно ехать в D (длина 3) и E (длина 4), причем кратчайший маршрут из A в E оказывается A-B-C-E (длина 7); «невыгодные» маршруты на схеме показывать не будем:
6)
из пункта D, кроме как в С и E, ехать некуда; путь D-C – это возврат назад (нас не интересует), путь D-E тоже не интересует, поскольку он дает длину 6 + 3 = 9, а мы уже нашли, что в E из A можно доехать по маршруту длины 7 7)
из пункта E можно ехать в F, длина полного маршрута 7 + 2 = 9
8) Ответ: 1
Пример задания: Между четырьмя местными аэропортами: ОКТЯБРЬ, БЕРЕГ, КРАСНЫЙ и СОСНОВО, ежедневно выполняются авиарейсы. Приведён фрагмент расписания перелётов между ними: Аэропорт вылета Аэропорт прилета Время вылета Время прилета СОСНОВО КРАСНЫЙ 06:20 08:35 КРАСНЫЙ ОКТЯБРЬ 10:25 12:35 ОКТЯБРЬ КРАСНЫЙ 11:45 13:30 БЕРЕГ СОСНОВО 12:15 14:25 СОСНОВО ОКТЯБРЬ 12:45 16:35 КРАСНЫЙ СОСНОВО 13:15 15:40 ОКТЯБРЬ СОСНОВО 13:40 17:25 ОКТЯБРЬ БЕРЕГ 15:30 17:15 СОСНОВО БЕРЕГ 17:35 19:30 БЕРЕГ ОКТЯБРЬ 19:40 21:55 Путешественник оказался в аэропорту ОКТЯБРЬ в полночь (0:00). Определите самое раннее время, когда он может попасть в аэропорт СОСНОВО. 1) 15:40 2) 16:35 3)17:15 4) 17:25 Решение: 1) для решения можно построить граф, показывающий, куда может попасть путешественник из аэропорта ОКТЯБРЬ 2) из аэропорта ОКТЯБРЬ есть три рейса: ОКТЯБРЬ СОСНОВО 13:40 17:25 ОКТЯБРЬ КРАСНЫЙ 11:45 13:30 ОКТЯБРЬ БЕРЕГ 15:30 17:15 3) построим граф, около каждого пункта запишем время прибытия
4) проверим, не будет ли быстрее лететь с пересадкой: рейс «КРАСНЫЙ-СОСНОВО» вылетает в 13:15, то есть, путешественник на него не успевает; он не успеет также и на рейс «БЕРЕГ-СОСНОВО», вылетающий в 12:15 5) таким образом, правильный ответ – 4 (прямой рейс).
A3 (базовый уровень, время – 2 мин) Тема: Построение таблиц истинности логических выражений. Что нужно знать: · условные обозначения логических операций · операцию «импликация» можно выразить через «ИЛИ» и «НЕ»: A → B = A Ú B или в других обозначениях A → B = · иногда для упрощения выражений полезны формулы де Моргана: (A Ù B) = A Ú B (A Ú B) = A Ù B · если в выражении нет скобок, сначала выполняются все операции «НЕ», затем – «И», затем – «ИЛИ», «импликация», и самая последняя – «эквивалентность» · таблица истинности выражения определяет его значения при всех возможных комбинациях исходных данных · если известна только часть таблицы истинности, соответствующее логическое выражение однозначно определить нельзя, поскольку частичной таблице могут соответствовать несколько разных логических выражений (не совпадающих для других вариантов входных данных); · количество разных логических выражений, удовлетворяющих неполной таблице истинности, равно · см. разбор задания А10 (стр.55) Пример задания: Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F: Какое выражение соответствует F?
2) X Ù Y Ù Z 3) X Ú Y Ú Z 4) X Ú Y Ú Z Решение (основной вариант): 1) нужно для каждой строчки подставить заданные значения X, Y и Z во все функции, заданные в ответах, и сравнить результаты с соответствующими значениями F для этих данных 2) если для какой-нибудь комбинации X, Y и Z результат не совпадает с соответствующим значением F, оставшиеся строчки можно не рассматривать, поскольку для правильного ответа все три результата должны совпасть со значениями функции F
(красный крестик показывает, что значение функции не совпадает с F, а знак «–» означает, что вычислять оставшиеся значения не обязательно).
Решение (вариант 2): 1) часто правильный ответ – это самая простая функция, удовлетворяющая частичной таблице истинности, то есть, имеющая единственный нуль или единственную единицу в полной таблице истинности 2) в этом случае можно найти такую функцию и проверить, есть ли она среди данных ответов 3) в приведенной задаче в столбце F есть единственный нуль для комбинации 4) выражение, которое имеет единственный нуль для этой комбинации, это 5) таким образом, правильный ответ – 4
A4 (базовый уровень, время – 1 мин) Тема: Файловая система. Что нужно знать: · маска служит для обозначения (выделения) группы файлов, имена которых имеют общие свойства, например, общее расширение · в масках, кроме «обычных» символов (допустимых в именах файлов) используются два специальных символа: звездочка «*» и знак вопроса «?»; · звездочка «*» обозначает любой количество любых символов, в том числе, может обозначать пустую последовательность; · знак вопроса «?» обозначает ровно один любой символ Пример задания: Определите, какое из указанных имен файлов удовлетворяет маске: ?hel*lo.c?* 1) hello.c 2) hello.cpp 3) hhelolo.cpp 4) hhelolo.c Решение: 1) будем проверять соответствие файлов маске по частям, записывая результаты в таблицу 2) начнем с первой части маски, «?hel»; эта часть означает, что перед сочетанием «hel» в начале имени стоит один любой символ; 3) сразу видим, что первые два имени не подходят (начинаются прямо с «hel», без стартового символа), отмечаем их крестиком в таблице и больше не рассматриваем:
желтым и фиолетовым маркером в таблице выделены соответствующие части маски и имен файлов (где есть совпадение) 4) для двух последних имен проверяем второй блок маски: после «hel» должна быть цепочка «lo.c», или вплотную (и это возможно!) или через произвольную «вставку», на которую указывает звездочка в маске; видим, что оба имени прошли проверку
5) последняя часть маски, «?*», означает, что после «lo.c» должен стоять по крайне мере один любой символ (на это указывает знак «?»); проверяя это правило, обнаруживаем, что для последнего имени, «hhelolo.c», маска не подходит, поскольку после «lo.c» ни одного символа нет:
6) таким образом, правильный ответ – 3.
Еще пример задания: Каталог содержит файлы с именами а) q.c б) qq.cpp в) qq.c г) q1.c1 д) qaa.cmd е) q12.cpp Определите, в каком порядке будут показаны файлы, если выбрана сортировка по типу (по возрастанию). 1) авгдбе 2) авгдеб 3) абвгде 4) авдбег Решение: 1) при сортировке по типу сравниваются расширения имен файлов 2) при сравнении используют коды символов 3) отсутствие символа (когда расширение закончилось) считается «меньше» любого символа, то есть, файл с расширением .с будет находиться в списке выше, чем файлы с расширениями .c1 и .cmd 4) коды цифр размещаются в таблице символов раньше, чем коды букв, то есть, файл с расширением .с1 будет находиться в списке выше, чем файл с расширением .сmd 5) теперь можно распределить имена файлов по расширениям а) q.c в) qq.c г) q1.c1 д) qaa.cmd б) qq.cpp е) q12.cpp 6) осталась еще одна проблема – решить, что делать, если расширения совпадают; в этом случае в большинстве программ для определенности используется дополнительная сортировка по имени, поэтому файл с именем q12.cpp будет стоять в списке выше, чем файл qq.cpp (код цифры ‘1' меньше, чем код буквы ‘q’) 7) в итоге получаем а) q.c в) qq.c г) q1.c1 д) qaa.cmd е) q12.cpp б) qq.cpp 8) таким образом, мы доказали, что правильный ответ – 2.
Еще пример задания: В каталоге находятся пять файлов:
|


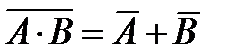

 , где
, где  – число отсутствующих строк; например, полная таблица истинности выражения с тремя переменными содержит 23=8 строчек, если заданы только 6 из них, то можно найти 28-6=22=4 разных логических выражения, удовлетворяющие этим 6 строчкам (но отличающиеся в двух оставшихся)
– число отсутствующих строк; например, полная таблица истинности выражения с тремя переменными содержит 23=8 строчек, если заданы только 6 из них, то можно найти 28-6=22=4 разных логических выражения, удовлетворяющие этим 6 строчкам (но отличающиеся в двух оставшихся)


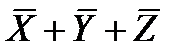
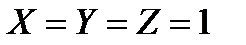
 , оно есть среди приведенных ответов (ответ 4)
, оно есть среди приведенных ответов (ответ 4)


