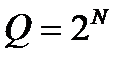Пример. Исходные трехзначные числа: 835, 196
Исходные трехзначные числа: 835, 196. Поразрядные суммы: 9, 12, 11. Результат: 12119 Определите, какое из следующих чисел может быть результатом работы автомата. 1) 151303 2) 161410 3) 191615 4) 121613 Решение: 1) итак, число строится из трех чисел, каждое из которых может быть однозначным (от 0 до 9) или двузначным (от 10 до 9 + 9 = 18) 2) если в числе 6 цифр, значит соединены три двузначных числа; в первом числе одно из них записывается как «03», что недопустимо (в этом случае правильное число было бы записано как 15133) 3) в третьем числе тоже 6 цифр: три двузначных числа, первое из которых равно 19, чего не может быть (никакие два однозначных числа не могут дать такую сумму) 4) в четвертом числе тоже 6 цифр: три числа 12, 16 и 13 расположены НЕ в порядке убывания, поэтому этот вариант неверен 5) во втором варианте никаких противоречий с условием нет 6) таким образом, ответ: 2. Еще пример задания: Предлагается некоторая операция над двумя произвольными трехзначными десятичными числами: 1) Записывается результат сложения старших разрядов этих чисел. 2) К нему дописывается результат сложения средних разрядов по такому правилу: если он меньше первой суммы, то полученное число приписывается к первому слева, иначе – справа. 3) Итоговое число получают приписыванием справа к числу, полученному после второго шага, сумму значений младших разрядов исходных чисел. Какое из перечисленных чисел могло быть построено по этому правилу? 1) 141819 2) 171418 3) 141802 4) 171814 Решение: 1) заметим, что сумма двух однозначных чисел – это число от 0 до 18 включительно 2) все предложенные числа шестизначные, поэтому все суммы, из которых составлены числа, должны быть двузначными 1) 141819 2) 171418 3) 141802 4) 171814 3) поскольку числа 19 быть не может (его не получить суммой двух однозначных чисел), этот вариант не подходит 4) из условия (2) следует, что первые два двузначных числа должны быть расположены по возрастанию (неубыванию), поэтому вариант 2 не подходит 5) при записи числа 2 ноль впереди не добавляется (в условии про это ничего не сказано), поэтому третий вариант тоже не подходит 6) вариант 4 удовлетворяет всем условиям. 7) таким образом, ответ: 4. A6 (базовый уровень, время – 3 мин) Тема: Поиск и сортировка информации в базах данных. Что нужно знать: · при составлении условия отбора можно использовать знаки отношений <, <= (меньше или равно), >, >= (больше или равно), = (равно), <> (не равно) · последовательность выполнения логических операций в сложных запросах: сначала выполняются отношения, затем – «И», потом – «ИЛИ» · для изменения порядка выполнения операции используют скобки Пример задания:
1) Иванов Т.М. 2) Черных И.А. 3) Цейс Т.Н. 4) Петренко Н.Н. Ещё пример задания: Результаты тестирования представлены в таблице:
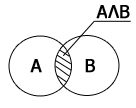
Сколько записей в ней удовлетворяют условию « Пол =’ж’ ИЛИ Химия > Биология »? 1) 5 2) 2 3) 3 4) 4 Решение: 1) заданное сложное условие отбора состоит из двух простых У1: Пол =’ж’ У2: Химия > Биология которые связаны с помощью логической операции «ИЛИ» 2) заметим, что столбцы «Фамилия», «Математика», «Русский язык» и «Информатика» никак не влияют на результат; уберем их из таблицы и добавим два новых столбца, в которых будем отмечать, выполняются ли условия У1 и У2 для каждой строчки
3) логическая операция «ИЛИ» означает выполнение хотя бы одного из двух условия (или обоих одновременно), поэтому заданному сложному условию удовлетворяют все строки, где есть хотя бы один плюс; таких строк пять, они выделены зеленым фоном:
4) таким образом, правильный ответ – 1. Еще пример задания: База данных о торговых операциях дистрибутора состоит из трех связанных таблиц. Ниже даны фрагменты этих таблиц. Таблица зарегистрированных дилеров
Таблица отгрузки товара
Таблица товаров
Сколько пачек бумаги было отгружено в Татарстан 5 января 2009 года? 1) 100 2) 200 3) 300 4) 1500 Решение: 1) уберем из таблиц всю лишнюю информацию; во-первых, нас интересует только бумага и только количество пачек, поэтому таблица товаров сводится к одной строчке
2) во-вторых, нас интересуют только дилеры из Татарстана, причем их названия и адреса не дают полезной информации, нужен только код; вот что остается от таблицы дилеров:
3) из таблицы отгрузки товара выбираем только информацию о поставках этим дилерам:
4) в последней таблице отмечаем строчки, которые относятся к бумаге (артикул 01002) и дате 5/01/2009:
5) таким образом, в 5/01/2009 в Татарстан было отгружено 300 упаковок бумаги 6) теперь вспоминаем, что в таблице товаров сказано, что в каждой упаковке 5 пачек, поэтому всего отгружено 1500 пачек 7) таким образом, правильный ответ – 4.
A7 (базовый уровень, время – 3 мин) Тема: Электронные таблицы. Что нужно знать: · адрес ячейки в электронных таблицах состоит из имени столбца и следующего за ним номера строки, например, C15 · формулы в электронных таблицах начинаются знаком = («равно») · · запись B2:C4 означает диапазон, то есть, все ячейки внутри прямоугольника, ограниченного ячейками B2 и C4 · например, по формуле =СУММ(B2:C4) вычисляется сумма значений ячеек B2, B3, B4, C2, C3 и C4 · в заданиях ЕГЭ могут использоваться стандартные функции СЧЕТ (количество непустых ячеек), СУММ (сумма), СРЗНАЧ (среднее значение), МИН (минимальное значение), МАКС (максимальное значение) · · адреса ячеек (или ссылки на ячейки) бывают относительные, абсолютные и смешанные, вся разница между ними проявляется при копировании формулы в другую ячейку. Пример задания: Дан фрагмент электронной таблицы:
Чему станет равным значение ячейки С2, если в нее скопировать формулу из ячейки С1? Знак $ обозначает абсолютную адресацию. 1) 40 2) 50 3)60 4) 70 Решение: 1) при копировании из C1 в C2 столбец не изменяется, а номер строки увеличивается на 1, поэтому в C2 получим формулу =A2+B$1 2) сумма ячеек A2 и B1 равна 30 + 20 = 50
Еще пример задания: Дан фрагмент электронной таблицы:
Как изменится значение ячейки С3, если после ввода формул переместить содержимое ячейки В2 в В3?(«+1» означает увеличение на 1, а «–1» – уменьшение на 1) 1) –2 2) –1 3) 0 4) +1 Решение: 1) это задача на знание особенностей функций СЧЕТ и СРЗНАЧ, которые не учитывают пустые ячейки 2) после ввода формул в С2 окажется количество непустых ячеек диапазона А1:В2, равное 4 3) в С3 будет выведено среднее значение диапазона А1:С2 равное (1+2+2+6+4)/5 = 3 4) после перемещения (не копирования!) содержимого ячейки В2 в В3 ячейка В2 окажется пустой, поэтому в С2 выводится число 3 – количество непустых ячеек диапазона А1:В2 5) в С3 будет выведено среднее значение диапазона А1:С2 равное (1+2+2+3)/4 = 2, то есть значение С3 уменьшится на 1 6) таким образом, правильный ответ – 2.
A8 (базовый уровень, время – 3 мин) Тема: Кодирование звука. Что нужно знать: · при оцифровке звука в памяти запоминаются только отдельные значения сигнала, который нужно выдать на динамик или наушники · частота дискретизации определяет количество отсчетов, запоминаемых за 1 секунду; 1 Гц (один герц) – это один отсчет в секунду, а 8 кГц – это 8000 отсчетов в секунду · глубина кодирования – это количество бит, которые выделяются на один отсчет · для хранения информации о звуке длительностью
· при двухканальной записи (стерео) объем памяти, необходимый для хранения данных одного канала, умножается на 2 Пример задания: Производится одноканальная (моно) звукозапись с частотой дискретизации 16 кГц и глубиной кодирования 24 бита. Запись длится 1 минуту, ее результаты записываются в файл, сжатие данных не производится. Какое из приведенных ниже чисел наиболее близко к размеру полученного файла, выраженному в мегабайтах? 1) 0,2 2) 2 3) 3 4) 4 Решение: 3) так как частота дискретизации 16 кГц, за одну секунду запоминается 16000 значений сигнала 4) так как глубина кодирования – 24 бита = 3 байта, для хранения 1 секунды записи требуется 16000 ´ 3 байта = 48 000 байт (для стерео записи – в 2 раза больше) 5) на 1 минуту = 60 секунд записи потребуется 60 ´ 48000 байта = 2 880 000 байт, то есть около 3 Мбайт 6) таким образом, правильный ответ – 3.
Еще пример задания: Производится одноканальная (моно) звукозапись с частотой дискретизации 64Гц. При записи использовались 32 уровня дискретизации. Запись длится 4 минуты 16 секунд, её результаты записываются в файл, причём каждый сигнал кодируется минимально возможным и одинаковым количеством битов. Какое из приведённых ниже чисел наиболее близко к размеру полученного файла, выраженному в килобайтах? 1) 10 2) 64 3) 80 4) 512 Решение: 1) так как частота дискретизации 64 Гц, за одну секунду запоминается 64 значения сигнала 2) глубина кодирования не задана! 3) используется 32 = 25 уровня дискретизации значения сигнала, поэтому на один отсчет приходится 5 бит 4) время записи 4 мин 16 с = 4 ´ 60 + 16 = 256 с 5) за это время нужно сохранить 256 ´ 5 ´ 64 бит = 256 ´ 5 ´ 8 байт = 5 ´ 2 Кбайт = 10 Кбайт 6) таким образом, правильный ответ – 1.
А9 (базовый уровень, время – 2 мин) Тема: Кодирование и декодирование информации. Что нужно знать: · кодирование – это перевод информации с одного языка на другой (запись в другой системе символов, в другом алфавите) · обычно кодированием называют перевод информации с «человеческого» языка на формальный, например, в двоичный код, а декодированием – обратный переход · один символ исходного сообщения может заменяться одним символом нового кода или несколькими символами, а может быть и наоборот – несколько символов исходного сообщения заменяются одним символом в новом коде (китайские иероглифы обозначают целые слова и понятия) · кодирование может быть равномерное и неравномерное; · закодированное сообщение можно однозначно декодировать с начала, если выполняется условие Фано: никакое кодовое слово не является началом другого кодового слова; · закодированное сообщение можно однозначно декодировать с конца, если выполняется обратное условие Фано: никакое кодовое слово не является окончанием другого кодового слова; · условие Фано – это достаточное, но не необходимое условие однозначного декодирования. Пример задания: Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, используется неравномерный двоичный код, позволяющий однозначно декодировать полученную двоичную последовательность. Вот этот код: А–00, Б–010, В–011, Г–101, Д–111. Можно ли сократить для одной из букв длину кодового слова так, чтобы код по-прежнему можно было декодировать однозначно? Коды остальных букв меняться не должны. Выберите правильный вариант ответа. 1) для буквы Б – 01 2) это невозможно 3) для буквы В – 01 4) для буквы Г – 01
Решение (1 способ, проверка условий Фано): 4) для однозначного декодирования достаточно, чтобы выполнялось условие Фано или обратное условие Фано; 5) проверяем последовательно варианты 1, 3 и 4; если ни один из них не подойдет, придется выбрать вариант 2 («это невозможно»); 6) проверяем вариант 1: А–00, Б–01, В–011, Г–101, Д–111. «прямое» условие Фано не выполняется (код буквы Б совпадает с началом кода буквы В); «обратное» условие Фано не выполняется (код буквы Б совпадает с окончанием кода буквы Г); поэтому этот вариант не подходит; 7) проверяем вариант 3: А–00, Б–010, В–01, Г–101, Д–111. «прямое» условие Фано не выполняется (код буквы В совпадает с началом кода буквы Б); «обратное» условие Фано не выполняется (код буквы В совпадает с окончанием кода буквы Г); поэтому этот вариант не подходит; 8) проверяем вариант 4: А–00, Б–010, В–011, Г–01, Д–111. «прямое» условие Фано не выполняется (код буквы Г совпадает с началом кодов букв Б и В); но «обратное» условие Фано выполняется (код буквы Г не совпадает с окончанием кодов остальных буквы); поэтому этот вариант подходит; 9) правильный ответ – 4. Решение (2 способ, дерево): 1)
построим двоичное дерево, в котором от каждого узла отходит две ветки, соответствующие выбору следующей цифры кода – 0 или 1; разместим на этом дереве буквы А, Б, В, Г и Д так, чтобы их код получался как последовательность чисел на рёбрах, составляющих путь от корня до данной буквы (красным цветом выделен код буквы В – 011):
2) здесь однозначность декодирования получается за счёт того, что при движении от корня к любой букве в середине пути не встречается других букв (выполняется условие Фано); 3) теперь проверим варианты ответа: предлагается перенести одну из букв, Б, В или Г, в узел с кодом 01, выделенный синим цветом 4) видим, что при переносе любой из этих букв нарушится условие Фано; например, при переносе буквы Б в синий узел она оказывается на пути от корня до В, и т.д.; это значит, что предлагаемые варианты не позволяют выполнить прямое условие Фано 5)
хочется уже выбрать вариант 2 («это невозможно»), но у нас есть еще обратное условие Фано, для которого тоже можно построить аналогичное дерево, в котором движение от корня к букве дает её код с конца (красным цветом выделен код буквы В – 011, записанный с конца): видно, что обратное условие Фано также выполняется, потому что на пути от корня к любой букве нет других букв 6) в заданных вариантах ответа предлагается переместить букву Б, В или Г в синий узел; понятно, что Б или В туда перемещать нельзя – перемещённая буква отказывается на пути от корня к букве Г; а вот букву Г переместить можно, при этом обратное условие Фано сохранится 7) правильный ответ – 4. Ещё пример задания: Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, решили использовать неравномерный двоичный код, позволяющий однозначно декодировать двоичную последовательность, появляющуюся на приёмной стороне канала связи. Использовали код: 1) 00 2) 01 3)11 4) 010 Решение: 8) заметим, что для известной части кода выполняется условие Фано – никакое кодовое слово не является началом другого кодового слова 9) если Д = 00, такая кодовая цепочка совпадает с началом Б = 000 и В = 001, невозможно однозначно раскодировать цепочку 000000: это может быть ДДД или ББ; поэтому первый вариант не подходит 10) если Д = 01, такая кодовая цепочка совпадает с началом Г = 011, невозможно однозначно раскодировать цепочку 011: это может быть ДА или Г; поэтому второй вариант тоже не подходит 11) если Д = 11, условие Фано тоже нарушено: кодовое слово А = 1 совпадает с началом кода буквы Д, невозможно однозначно раскодировать цепочку 111: это может быть ДА или ААА; третий вариант не подходит 12) для четвертого варианта, Д = 010, условие Фано не нарушено; 13) правильный ответ – 4.
Еще пример задания: Для кодирования букв А, Б, В, Г решили использовать двухразрядные последовательные двоичные числа (от 00 до 11, соответственно). Если таким способом закодировать последовательность символов БАВГ и записать результат шестнадцатеричным кодом, то получится 1) 4B16 2) 41116 3)BACD16 4) 102316 Решение: 14) из условия коды букв такие: A – 00, Б –01, В – 10 и Г – 11, код равномерный 15) последовательность БАВГ кодируется так: 01 00 10 11 = 1001011 16) разобьем такую запись на тетрады справа налево и каждую тетраду переведем в шестнадцатеричную систему (то есть, сначала в десятичную, а потом заменим все числа от 10 до 15 на буквы A, B, C, D, E, F); получаем 1001011 = 0100 10112 = 4B16 17) правильный ответ – 1.
A10 (повышенный уровень, время – 2 мин) Тема: Основные понятия математической логики. Что нужно знать: · условные обозначения логических операций · таблицы истинности логических операций «И», «ИЛИ», «НЕ», «импликация» · операцию «импликация» можно выразить через «ИЛИ» и «НЕ»: A → B = A Ú B или в других обозначениях A → B = · если в выражении нет скобок, сначала выполняются все операции «НЕ», затем – «И», затем – «ИЛИ», и самая последняя – «импликация» · иногда полезны формулы де Моргана[*]: (A Ù B) = A Ú B (A Ú B) = A Ù B · основные сведения о логических операциях:
· порядок выполнения логических операций: 1. B 2. (B)∧C 3. A∨ ((B)∧C) 4. (A∨((B)∧C))→D 5. ((A∨((B)∧C))→D)↔E Пример задания: Какое из приведённых имен удовлетворяет логическому условию: 1) КРИСТИНА 2) МАКСИМ 3) СТЕПАН 4) МАРИЯ Решение: 7) два условия связаны с помощью операции /\ («И»), поэтому должны выполняться одновременно 8) импликация ложна, если ее первая часть («посылка») истинна, а вторая («следствие») – ложна 9) первое условие «первая буква согласная → вторая буква согласная» ложно тогда, когда первая буква согласная, а вторая – гласная, то есть для ответов 2 и 4 10) второе условие «предпоследняя буква гласная → последняя буква гласная» ложно тогда, когда предпоследняя буква гласная, а последняя – согласная, то есть, для ответа 3 11) таким образом, для варианта 1 (КРИСТИНА) оба промежуточных условия и исходное условие в целом истинны 12) ответ: 1. Ещё пример задания: Для какого из указанных значений X истинно высказывание ((X > 2)→(X > 3))? 1) 1 2) 2 3) 3 4) 4 Решение (вариант 1, прямая подстановка): 13) определим порядок действий: сначала вычисляются результаты отношений в скобках, затем выполняется импликация (поскольку есть «большие» скобки), затем – отрицание (операция «НЕ») для выражения в больших скобках 14) выполняем операции для всех приведенных возможных ответов (1 обозначает истинное условие, 0 – ложное); сначала определяем результаты сравнения в двух внутренних скобках:
15) по таблице истинности операции «импликация» находим третий столбец (значение выражения в больших скобках), применив операцию «импликация» к значениям второго и третьего столбцов (в каждой строке):
16) значение выражения равно инверсии третьего столбца (меняем 1 на 0 и наоборот):
17) таким образом, ответ – 3.
А11 (повышенный уровень, время – 3 мин) Тема: Вычисление информационного объема сообщения. Что нужно знать: · с помощью K бит можно закодировать · таблица степеней двойки, она же показывает, сколько вариантов Q можно закодировать с помощью K бит:
· при измерении количества информации принимается, что в одном байте 8 бит, а в одном килобайте (1 Кбайт) – 1024 байта, в мегабайте (1 Мбайт) – 1024 Кбайта[‡] · чтобы найти информационный объем сообщения (текста) I, нужно умножить количество символов (отсчетов) N на число бит на символ (отсчет) K: · две строчки текста не могут занимать 100 Кбайт в памяти · мощность алфавита M – это количество символов в этом алфавите · если алфавит имеет мощность M, то количество всех возможных «слов» (символьных цепочек) длиной N (без учета смысла) равно Пример задания: Для регистрации на сайте некоторой страны пользователю требуется придумать пароль. Длина пароля – ровно 11 символов. В качестве символов используются десятичные цифры и 12 различных букв местного алфавита, причём все буквы используются в двух начертаниях: как строчные, так и заглавные (регистр буквы имеет значение!). Под хранение каждого такого пароля на компьютере отводится минимально возможное и одинаковое целое количество байтов, при этом используется посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством битов. Определите объём памяти, который занимает хранение 60 паролей. 1) 540 байт 2) 600 байт 3) 660 байт 4) 720 байт Решение: 10) согласно условию, в пароле можно использовать 10 цифр (0..9) + 12 заглавных букв местного алфавита + 12 строчных букв, всего 10 + 12 + 12 = 34 символа 11) для кодирования 34 символов нужно выделить 6 бит памяти (5 бит не хватает, они позволяют закодировать только 25 = 32 варианта) 12) для хранения всех 11 символов пароля нужно 11 × 6 = 66 бит 13) поскольку пароль должен занимать целое число байт, берем ближайшее большее (точнее, не меньшее) значение, которое кратно 8: это 72 = 9 × 8; то есть один пароль занимает 9 байт 14) тогда 60 паролей занимают 9 × 60 = 540 байт 15) ответ: 1.
Ещё пример задания: В велокроссе участвуют 119 спортсменов. Специальное устройство регистрирует прохождение каждым из участников промежуточного финиша, записывая его номер с использованием минимально возможного количества бит, одинакового для каждого спортсмена. Каков информационный объем сообщения, записанного устройством, после того как промежуточный финиш прошли 70 велосипедистов? 1) 70 бит 2) 70 байт 3) 490 бит 4) 119 байт Решение: 16) велосипедистов было 119, у них 119 разных номеров, то есть, нам нужно закодировать 119 вариантов 17) по таблице степеней двойки находим, что для этого нужно минимум 7 бит (при этом можно зак
|

 знаки +, –, *, / и ^ в формулах означают соответственно сложение, вычитание, умножение, деление и возведение в степень
знаки +, –, *, / и ^ в формулах означают соответственно сложение, вычитание, умножение, деление и возведение в степень функция СРЗНАЧ при вычислении среднего арифметического не учитывает пустые ячейки и ячейки, заполненные текстом; например, после ввода формулы в C2 появится значение 2 (ячейка А2 – пустая) функция СЧЕТ(A1:B2) в этом случае выдаст значение 3 (а не 4).
функция СРЗНАЧ при вычислении среднего арифметического не учитывает пустые ячейки и ячейки, заполненные текстом; например, после ввода формулы в C2 появится значение 2 (ячейка А2 – пустая) функция СЧЕТ(A1:B2) в этом случае выдаст значение 3 (а не 4). секунд, закодированном с частотой дискретизации
секунд, закодированном с частотой дискретизации  Гц и глубиной кодирования
Гц и глубиной кодирования  бит требуется
бит требуется  бит памяти; например, при
бит памяти; например, при  кГц, глубине кодирования 16 бит на отсчёт и длительности звука 128 секунд требуется
кГц, глубине кодирования 16 бит на отсчёт и длительности звука 128 секунд требуется бит
бит байт
байт Кбайт
Кбайт Мбайт
Мбайт
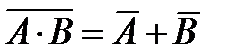





 различных вариантов (чисел)
различных вариантов (чисел)
 ; для двоичного кодирования (мощность алфавита M – 2 символа) получаем известную формулу:
; для двоичного кодирования (мощность алфавита M – 2 символа) получаем известную формулу: