Умножь на 3
Первая из них увеличивает число на экране на 1, вторая – утраивает его. Программа для Утроителя – это последовательность команд. Сколько есть программ, которые число 1 преобразуют в число 20? Ответ обоснуйте. Решение (1 способ, составление таблицы): 1) заметим, что при выполнении любой из команд число увеличивается (не может уменьшаться) 2) начнем с простых случаев, с которых будем начинать вычисления: для чисел 1 и 2, меньших, чем 3, существует только одна программа, состоящая только из команд сложения; если через 3) теперь рассмотрим общий случай, чтобы построить рекуррентную формулу, связывающую 4) если число N не делится на 3, то оно могло быть получено только последней операцией сложения, поэтому 5) если N делится на 3, то последней командой может быть как сложение, так и умножение 6) поэтому для получения если N не делится на 3: если N делится на 3: 7) остается заполнить таблицу для всех значений от 1 до N:
8) Заметим, что количество вариантов меняется только в тех столбцах, где N делится на 3, поэтому из всей таблицы можно оставить только эти столбцы:
9) заданное число 20 попадает в последний интервал (от 18 до 21), поэтому … 10) ответ – 12. Решение (2 способ, подстановка – вычисления по формулам «с конца»): 1) п. 1-6 выполняются так же, как и при первом способе; главная задача – получить рекуррентную формулу: если N не делится на 3: если N делится на 3: с начальными условиями 2) начинаем с заданного конечного числа 20; применяем первую формулу (
3) далее применяем вторую формулу (
4) применяем первую формулу для 17:
5) применяем вторую формулу для обоих слагаемых:
где учтено, что 6) с помощью первой формулы переходим в правой части к числам, делящимся на 3:
а затем применяем вторую формулу для каждого слагаемого
7) снова используем первую формулу
а затем – вторую:
8) и еще раз
9) ответ – 12. Решение (3 способ, О.В. Шецова, лицей № 6, г. Дубна): 1) будем составлять таблицу из трех столбцов: в первом записывается получаемое число от 1 до 20, во втором – какой последней командой может быть получено это число, а в третьем вычисляем количество различных программ для получения этого числа из 1 2) очевидно, что число 1 может быть получено с помощью одной единственной (пустой) программы:
3) число 2 не делится на 3, поэтому его можно получить только командой сложения (+1), значит, количество программ для 2 совпадает с количеством программ для 1:
4) число 3 делится на 3, поэтому его можно получить с помощью двух команд: +1 (из 2) и *3 (из 1):
5) числа 4 и 5 не делятся на 3, поэтому их можно получить только с помощью команды +1, а число 6 может быть получено двумя командами:
6) следующая группа – 7, 8 (не делятся на 3) и 9 (делится на 3):
7) далее – 10, 11 и 12:
8) и так далее, вот полностью заполненная таблица (до конечного числа 20):
9) ответ – количество программ, с помощью которых можно получить число 20 из 1, – считываем из последней ячейки третьего столбца 10) ответ – 12.
Еще пример задания: У исполнителя Калькулятор две команды, которым присвоены номера:
|

 обозначить количество разных программ для получения числа N из 1, то
обозначить количество разных программ для получения числа N из 1, то  .
.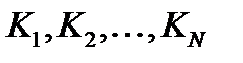 , то есть с решениями таких же задач для меньших N
, то есть с решениями таких же задач для меньших N
 (количество программ с последней командой сложения) и
(количество программ с последней командой сложения) и  (количество программ с последней командой умножения). В итоге получаем:
(количество программ с последней командой умножения). В итоге получаем:

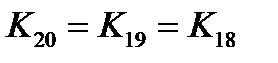

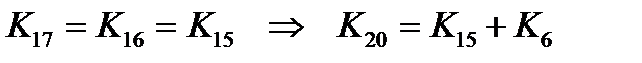






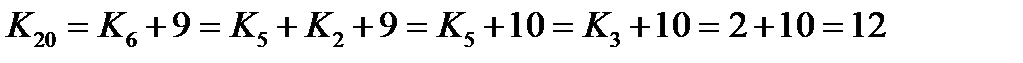
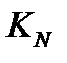 , но тогда мы фактически придем к табличному методу
, но тогда мы фактически придем к табличному методу



