Увеличь вторую с конца цифру на 1
Первая из них увеличивает число на экране на 1, вторая – увеличивает на 1 число десятков. Если перед выполнением команды 2 вторая с конца цифра равна 9, она не изменяется. Программа для Калькулятора – это последовательность команд. Сколько есть программ, которые число 15 преобразуют в число 28? Ответ обоснуйте. Решение (составление таблицы): 1) заметим, что при выполнении любой из команд число увеличивается (не может уменьшаться) 2) при заданных командах очередное число N может быть получено двумя способами: 3) увеличением на 1 (для всех чисел, больших начального числа) 4) увеличением числа десятков на 1 (то есть, фактически командой «+10») – для всех чисел, больших или равных 25; например, число 24 не может быть получено этой командой (14 + 10 = 24), потому что число 14 меньше, чем начальное значение 15 5) таким образом, рекуррентные формулы принимают вид
6) других способов получения числа с помощью исполнителя с заданными командами нет, то есть мы таким образом рассматриваем все возможные программы 7) начальное значение: 8) далее заполняем таблицу:
9) Ответ: 5 C4 (высокий уровень, время – 60 мин) Тема: Обработка данных, вводимых в виде символьных строк (написать программу средней сложности из 30-50 строк) или последовательности чисел. Что нужно знать: · символьная строка – это цепочка символов, которая может обрабатываться как единое целое · для обращения к символу с номером i строки s используется запись s[i], это говорит о том, что строка – особый вариант массива, в котором хранятся символы · знак сложения при работе с символьными строками означает сцепку, объединение двух строк в одну (добавление второй строки в конец первой), например: s:= '123' + '456'; { получили '123456' } · с помощью функции Ord можно получить код символа; цифры имеют коды от 48 (цифра 0) до 57 (цифра 9), например k:= Ord('1'); { получили 49 } то же самое можно сделать с помощью преобразования типа k:= integer('1'); { получили 49 } · с помощью функции Chr можно сделать обратный переход: получить символ по его коду, например c:= Chr(49); { получили символ '1' } то же самое можно сделать с помощью преобразования типа (привести integer к char) c:= char(49); { получили символ '1' } · для работы со строками в наиболее распространенных Паскаль-средах используют стандартные функции (здесь s – это переменная типа string, символьная строка; n и r – целые переменные)
и процедуры
· структура (в Паскале она называется «запись», record) – это сложный тип данных, который может включать в себя несколько элементов – полей; поля могут иметь различный тип · записи в Паскале объявляются с помощью ключевого слова record; в простейшем случае можно выделить память под одну запись так: var x: record name: string; code: integer; End; эта запись состоит из двух полей: символьной строки name и целого числа code · записи очень удобны для работы, когда все данные в целом представляют собой единый блок информации, например, данные об ученике; если не использовать записи, было бы нужно выделять в памяти отдельно символьную строку и отдельно целую переменную, причем эти данные внешне были бы никак не связаны, поэтому программа с записями часто получается логичнее и понятнее как для автора, так и для того, кто будет в ней разбираться · для обращения к полям записи используют точку, например x.name означает «поле name записи x» · можно сразу объявить массив записей: var Info: array[1..100] of record name: string; code: integer; End; это 100 одинаковых записей, имеющих общее имя Info и расположенных в памяти рядом; в каждой структуре есть поля nаme и code; чтобы работать с полями записи с номером k используют обращения вида Info[k].name и Info[k].code Сложность алгоритмов: · обозначение · сложность · количество операций для алгоритма, имеющего сложность · если в одном алгоритме решения задачи используется несколько циклов от 1 до N, а во втором – только один цикл, то алгоритм с одним циклом, как правило, эффективнее (хотя оба алгоритма имеют сложность · для алгоритма, имеющего сложность · при больших N функция · иногда встречаются алгоритмы сложности · для многих задач известны только алгоритмы экспоненциальной сложности, когда размер массива входит в показатель степени, например Пример задания: На вход программе подаются сведения о номерах школ учащихся, участвовавших в олимпиаде. В первой строке сообщается количество учащихся N, каждая из следующих N строк имеет формат: <Фамилия> <Инициалы> <номер школы>; где <Фамилия> – строка, состоящая не более чем из 20 символов, <Инициалы> – строка, состоящая из 4-х символов (буква, точка, буква, точка), <номер школы> – не более чем двузначный номер. <Фамилия> и <Инициалы>, а также <Инициалы> и <номер школы> разделены одним пробелом. Пример входной строки:
|

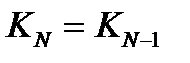 для всех чисел, меньших, чем 25
для всех чисел, меньших, чем 25 для чисел, больших или равных 25
для чисел, больших или равных 25 (число 15 можно получить единственной пустой программой)
(число 15 можно получить единственной пустой программой)

 говорит о том, что при увеличении в 2 раза размера массива данных количество операций тоже увеличивается примерно в 2 раза (для больших N)
говорит о том, что при увеличении в 2 раза размера массива данных количество операций тоже увеличивается примерно в 2 раза (для больших N) , где a и b – некоторые постоянные
, где a и b – некоторые постоянные в каждом случае своя, для алгоритма с несколькими циклами она будет больше)
в каждом случае своя, для алгоритма с несколькими циклами она будет больше) , количество операций пропорционально квадрату размера массива, то есть, если N увеличить в 2 раза, то количество операций увеличивается примерно в 4 раза (например, в программе используется два вложенных цикла, в каждом из которых N шагов); сложность
, количество операций пропорционально квадрату размера массива, то есть, если N увеличить в 2 раза, то количество операций увеличивается примерно в 4 раза (например, в программе используется два вложенных цикла, в каждом из которых N шагов); сложность  растет значительно быстрее, чем
растет значительно быстрее, чем  , поэтому алгоритм, имеющий сложность
, поэтому алгоритм, имеющий сложность  (три вложенных цикла от 1 до N), при больших N они работают медленнее, чем любой алгоритм сложности
(три вложенных цикла от 1 до N), при больших N они работают медленнее, чем любой алгоритм сложности  , для больших N такие задачи не решаются за приемлемое время (например, «взламывание» шифров)
, для больших N такие задачи не решаются за приемлемое время (например, «взламывание» шифров)


