Эмпирическая функция распределения
Функция
Функция Функция Оценкой для плотности распределения непрерывной случайной величины
Выборочные характеристики статистических распределений Для описания основных свойств статистических распределений используют выборочные характеристики двух видов: средние и вариации (рассеяния). К средним относятся: · средняя арифметическая:
Применяется к вариационному ряду с несгруппированными данными наблюдения; · взвешенная средняя арифметическая (частоты
или
Применяется к ранжированному вариационному ряду дискретного признака Х. · медиана – это серединное значение признака Х, по определению
· мода – наиболее часто встречающееся значение признака
|
или 
называется эмпирической функцией распределения.
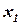
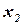
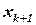
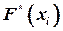
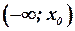
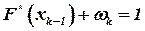
неубывающая, ее график имеет ступенчатый вид, т.е. представляет собой отрезки прямых, параллельных оси абсцисс, длина отрезков: 
расстояние от отрезков до оси абсцисс: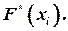 
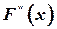служит оценкой неизвестной функцией распределения 
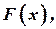т.е.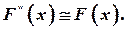 
(признака 
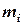и частости 
называют весами):
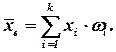
если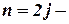 
четное;
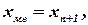если 
нечетное.
если 
