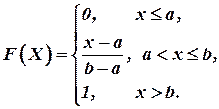Модой  случайной величины
случайной величины  называется такое ее значение, для которого
называется такое ее значение, для которого
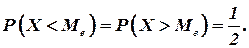
| (6.17)
|
Медиану  находят из условия
находят из условия

| (6.18)
|
Некоторые дискретные распределения
Биномиальный закон распределения
ДСВ  имеет биномиальный закон распределения, если она принимает значения
имеет биномиальный закон распределения, если она принимает значения  с вероятностями
с вероятностями

| (7.1)
|
где 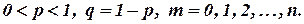
Числовые характеристики биномиального распределения:

| (7.2)
|

| (7.3)
|
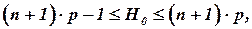
| (7.4)
|
где  целое число; целое число;
| |
| Коэффициент вариации
| |

| (7.5)
|
| Коэффициент асимметрии
| |

| (7.6)
|
| Коэффициент эксцесса
| |

| (7.7)
|
Закон распределения Пуассона
Дискретная случайная величина  имеет закон распределения Пуассона, если она принимает значения
имеет закон распределения Пуассона, если она принимает значения 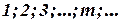 (бесконечное, но счетное множество) с вероятностями
(бесконечное, но счетное множество) с вероятностями

| (7.8)
|

| (7.9)
|

| (7.10)
|

| (7.11)
|

| (7.12)
|
 определить по таблице.
определить по таблице.
Геометрическое распределение
ДСВ  имеет геометрическое распределение, если она принимает значения
имеет геометрическое распределение, если она принимает значения 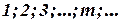 (бесконечное, но счетное множество) с вероятностями
(бесконечное, но счетное множество) с вероятностями

| (7.13)
|
Характеристики:

| (7.14)
|

| (7.15)
|
Гипергеометрическое распределение
ДСВ  имеет гипергеометрическое распределение, если она принимает значения
имеет гипергеометрическое распределение, если она принимает значения 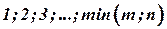 с вероятностями
с вероятностями

| (7.16)
|
Характеристики:

| (7.17)
|

| (7.18)
|
Непрерывные распределения
| Название
распределения
| Функция распределения
(закон, график)
| Плотность распределения (закон, график)
| Параметр
| Числовые
характеристики
|
| Равномерный закон
| 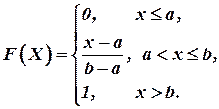
| 
| а, b
| 


|

| 
|
| Показательный закон
| 
| 
| 
| 

|

| 
|
| Нормальный
закон
| 
| 
| 
| 

|

| 
|

 случайной величины
случайной величины  называется такое ее значение, для которого
называется такое ее значение, для которого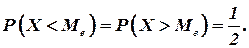
 находят из условия
находят из условия
 с вероятностями
с вероятностями
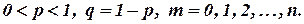


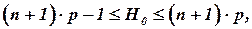
 целое число;
целое число;



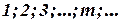 (бесконечное, но счетное множество) с вероятностями
(бесконечное, но счетное множество) с вероятностями




 определить по таблице.
определить по таблице.


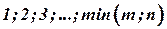 с вероятностями
с вероятностями