Выполнение. В SPSS существует возможность проверить, соответствует ли реальное распределение переменной нормальному

В SPSS существует возможность проверить, соответствует ли реальное распределение переменной нормальному, равномерному, экспоненциальному распределению или распределению Пуассона, при помощи теста Колмогорова–Смирнова.

Чтобы продемонстрировать работу данного теста, проверим на предмет наличия нормального распределения исходные значения переменной Х (количество опозданий работников цеха за отчетные месяцы) из предыдущей работы.

Выберем в меню Analyze (Анализ) Nonparametric Tests (Непараметрические тесты) 1–Sample KS (К–С одной выборки).

Появится диалоговое окно One Sample Kolmogorov–Smirnov Test (Тест Колмогорова–Смирнова для одной выборки) (рис. 2.3.2).

 

 

Рис. 2.3.2. Диалоговое окно

«Тест Колмогорова–Смирнова для одной выборки»

 

Перенесем переменную x в поле тестируемых переменных.

Если щелкнуть по кнопке Options (Установки), то можно дополнительно организовать вывод характеристик дескриптивной статистики и квартилей.

Щелкнем на OK.

В окне просмотра появятся следующие результаты.

 

Рис. 2.3.3. Результаты теста Колмогорова–Смирнова

 

Полученные результаты включают:

· среднее значение и стандартное отклонение;

· промежуточные результаты, полученные при выполнении теста Колмогорова–Смирнова;

· вероятность ошибки p.

Отклонение от нормального распределения считается существенным при значении р < 0,05; в этом случае для соответствующих переменных следует применять непараметрические тесты.

В рассматриваемом примере (значение р = 0,317), то есть вероятность ошибки является не значимой; поэтому значения переменной достаточно хорошо подчиняются нормальному распределению.

Аналогично можно провести анализ и по остальным видам распределения.

Выяснить, отличается ли среднее значение, полученное на основе данной выборки, от предварительно заданного контрольного значения, позволяет T –тест одной выборки.

Мы проверим, отличается ли средний показатель количества опозданий работников цеха за отчетные месяцы, полученный при нашем исследовании, от значения 7,32, которое могло быть определено в каком–либо другом исследовании (по правилу трех сигм для нормального закона с точностью 0,997 весь диапазон разброса случайной величины заключен в пределах ± 3σ от центра величины).

Выберем в меню команды Analyze (Анализ) Compare Means (Сравнение средних) One–Sample T Test (Одновыборочный T критерий).

Откроется диалоговое окно One–Sample T Test (Одновыборочный T критерий) (рис. 2.3.4).

 

 

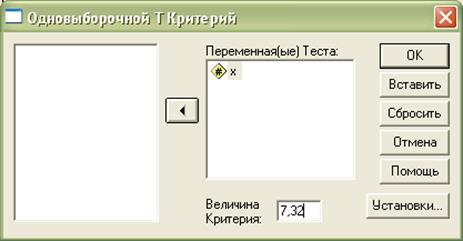
Рис. 2.3.4. Диалоговое окно «Одновыборочный T –критерий»

 

Перенесем переменную Х в поле Test Variable(s) (Переменная(ые) Теста) и введем в поле Test Value (Величина Критерия) значение 7,32.

Кнопкой Options (Установки) можно задать вместо 95% любой другой доверительный интервал.

Значение доверительного интервала может принимать значения в промежутке от 1 до 99%. Запустим вычисления, щелкнув OK.

 

Рис. 2.3.5. Результаты T –теста

 

Результаты, показанные в окне просмотра, свидетельствуют о том, что в данном исследовании среднее исходное количество опозданий работников цеха за отчетные месяцы, что составляет 6,186, значимо (р = 0,007) отличается от контрольного значения 7,32.