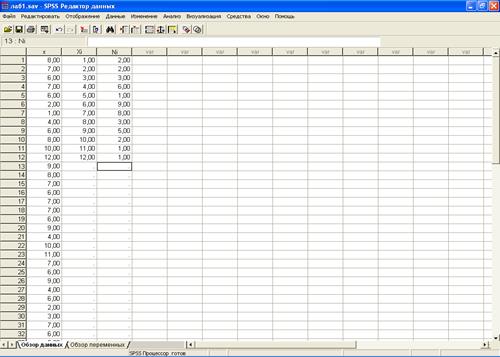
Выполнение. Для начала представим графически выборку.
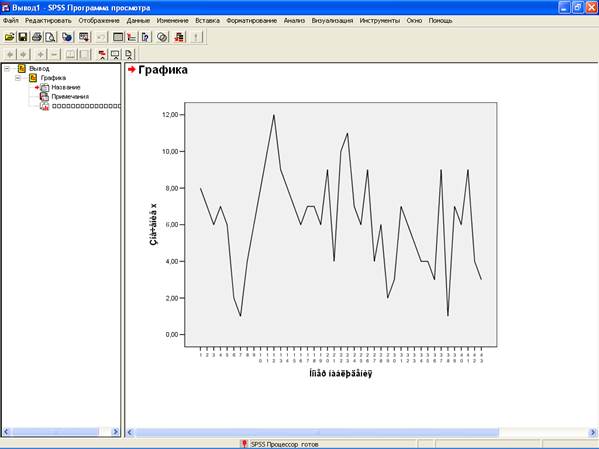
Для начала представим графически выборку. В меню выберем Graphs (Визуализация) Line (Линия) выберем Simple (Простой), в поле Data in Chart Are (Данные для графика) выберем Values of individual cases (Значения отдельных наблюдений) Define (Определить). В появившемся окне Define Simple из левого списка переместим кнопкой–стрелкой х в поле Line Represent. Нажмем OK. Получили следующий график (рис. 2.1.1), который представляет линию выборки.
Рис. 2.1.1. Линия выборки
Теперь поострим гистограмму значений. В меню выберем Graphs (Визуализация) Histogram (Гистограмма) и занесем в строку Variable (Переменная) x (рис. 2.1.2).
Рис. 2.1.2. Гистограмма значений
Первым этапом статистического анализа данных, как правило, является частотный анализ и получение основных параметров исследуемой величины. Предварительный анализ данных включает в себя вычисление основных параметров, характеризующих переменные (математическое ожидание, среднеквадратичное отклонение, дисперсия, минимум, максимум и т.д.), составление таблиц частот для одной или нескольких переменных. Выберем в меню Analyze (Анализ) Statistics (Статистика) Frequencies (Частоты), появится диалоговое окно Frequencies (Частоты) (рис. 2.1.4).
Рис. 2.1.3. Фрагмент файла данных
Рис. 2.1.4. Вид диалогового окна Frequencies (Частоты)
Кнопкой с треугольником перенесем переменную x в список выходных переменных. Для получения основных параметров, характеризующих переменную щелкнем в диалоговом окне Frequencies (Частоты) на кнопке Statistics (Статистика). Откроется диалоговое окно Frequencies: Statistics (Частоты: Статистика). В текущем диалоговом окне выберем интересующие нас пункты. В группе Central Tendency (Средние) выберем следующие характеристики: Mean (Среднее значение), Median (Медиана). В группе Dispersion (Разброс) выберем следующие меры разброса: Std. deviation (Стандартное отклонение), Variance (Дисперсия), Minimum (Минимум), Maximum (Максимум). Для продолжения расчетов нажмем кнопку Continue (Продолжить). Для графического представления имеющихся данных щелкнем на кнопке Charts (Диаграммы). Откроется диалоговое окно Frequencies: Charts (Частоты: Диаграммы). Выберем в группе Chart Type (Тип диаграммы) пункт Bar Charts (Столбчатая диаграмма), а в группе Chart Values (Значения диаграммы) – пункт Frequencies (Частота). Подтвердим выбор кнопкой Continue и вернемся в диалоговое окно Frequencies. Подтвердим операцию нажатием кнопки ОК в диалоговом окне Frequencies (Частоты). Вывод основных результатов выглядит следующим образом (рис. 2.1.5).
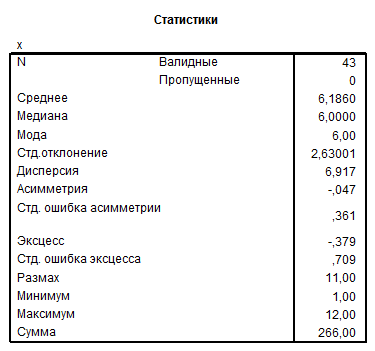
Рис. 2.1.5. Результаты выполнения процедуры В первой из таблиц представлены основные статистические параметры, характеризующие исследуемый показатель урожайности x. Видно, что математическое ожидание Во второй таблице можно увидеть частотное распределение исследуемой величины, т.е. каждая строка частотной таблицы описывает одно возможное значение. Теперь возможно построение полигона. Полигон – это ломаная, соединяющая точки (xi; ni). Для этого скопируем из окна просмотра результатов в редактор данных 1 и 2 столбцы в таблице x. Для этого необходимо дважды кликнуть левой кнопкой мыши в нужном столбце, выделив соответствующие значения, скопируем их. Вернемся в редактор данных, поставим указатель мыши в любой из свободных столбцов, расположенных правее столбца значений x, и вставим скопированные значения. Аналогично сделаем с частотами. Для простоты переименуем VAR00001 в xi и VAR00002 – ni. Для чего необходимо дважды кликнуть левой кнопкой мыши по VAR00001, или перейти на вкладку «Обзор переменных», и в соответствующих строках ввести соответствующее значение. Теперь редактор переменных выглядит, как показано на рисунке 2.1.6.
Рис. 2.1.6. Редактор данных Для построения полигона частот необходимо выбрать Graphs (Визуализация) Scatter (Разброс/точка) Simple (Простой) Define (Определить). В определении переменных выбираем за ось Y – ni за ось X – xi – OK. В редакторе графиков изменяем значения метки ○ на *, дважды кликнув по любой из метки и установив соответствующее значение метки. Теперь график выглядит как на рис. 2.1.7.
Рис. 2.1.7. Полигон частот
|





 , медиана
, медиана 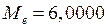 , среднее квадратическое отклонение
, среднее квадратическое отклонение  , дисперсия
, дисперсия  , также приведены максимальное и минимальное значение исследуемого показателя.
, также приведены максимальное и минимальное значение исследуемого показателя.