Выполнение. В рамках однофакторного дисперсионного анализа предусмотрена процедура One–Way ANOVA, которая заключается в анализе влияния одного качественного фактора на
В рамках однофакторного дисперсионного анализа предусмотрена процедура One–Way ANOVA, которая заключается в анализе влияния одного качественного фактора на количественную переменную. Требуется указать список количественных переменных и фактор, от которого они зависят. Имеем задачу однофакторного дисперсионного анализа с наблюдениями на трех уровнях. Качественным показателем, влияющим на количественную переменную (прибыль по филиалам), является номер филиала предприятия. Выполним следующие действия. · Создадим и загрузим файл данных (рис. 2.5.1).
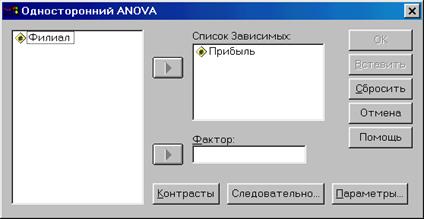
Рис. 2.5.1. Фрагмент файла данных · Выберем в меню команды Analyze (Анализ) Compare Means (Сравнение средних) One–Way ANOVA (Однофакторный дисперсионный анализ). Появится диалоговое окно односторонний ANOVA (рис. 2.5.2). · Перенесем переменную Прибыль в список зависимых переменных, a переменную Филиал – в поле «Фактор». · Зададим вывод описательной статистики, для этого щелкнем на кнопке «Параметры» и в открывшемся окне (рис. 2.5.3) установим флажок «Описательный».
Рис. 2.5.2. Диалоговое окно «Однофакторный дисперсионный анализ»
Рис. 2.5.3. Диалоговое окно «Однофакторный дисперсионный анализ: Опции»
Запустим тест, щелкнув на ОК. Получим следующие результаты.
ANOVA Прибыль
Рис. 2.5.4. Результат выполнения процедуры
Таким образом, имеем следующие характеристики: · · Средние значения переменной на i –м уровне · Среднее значение переменной по всем значениям · Сумму квадратов отклонений всех наблюдений от общего среднего · Сумму квадратов отклонений средних групповых значений · Остаточную сумму квадратов отклонений
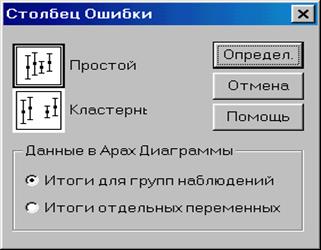
Отметим справедливость соотношения Нулевая гипотеза принимается при. Проверим гипотезу для уровня 0,05: Имеем, что Наглядным представлением результатов являются графики средних значений и их доверительных интервалов (простая диаграмма величины ошибки) (рис.2.5.7). Построим подобный график, для этого выполним следующие действия: · Выберем команду «Визуализация/Колонка ошибок» и в открывшемся окне (рис. 2.5.5) выберем вариант «Простой» и нажмем на кнопку «Определ.». · В появившемся диалоговом окне (рис. 2.5.6) заполним следующие поля. Переменная в рассматриваемом случае это переменная Прибыль. Ось категорий – поле факторной переменной (переменной, содержащей категории), для данного примера это переменная Филиал. Изобразить панели – что следует отразить на графике: доверительный интервал для математического ожидания, стандартную ошибку математического ожидания или среднеквадратичное отклонение. Нас интересует доверительный интервал для математического ожидания. Уровень – пределы доверительного интервала (по умолчанию стоит значение 95%).
Рис. 2.5.5. Диалоговое окно «Колонка Ошибок»
Рис. 2.5.6. Диалоговое окно
Запустим выполнение, щелкнув на ОК. Получим следующий график (рис. 2.5.7).
Рис. 2.5.7. Результат выполнения процедуры «Визуализация/Колонка ошибок»
|




 .
.  .
.
 .
.
 .
.

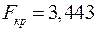 ;
;  .
. , нулевую гипотезу отвергаем и делаем вывод, что работа в каждом из филиалов влияет на месячную прибыль предприятия.
, нулевую гипотезу отвергаем и делаем вывод, что работа в каждом из филиалов влияет на месячную прибыль предприятия.