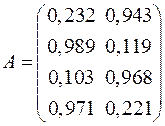Выполнение. · Создадим файл данных, присваивая каждой переменной результаты успеваемости студентов по конкретному предмету.
· Создадим файл данных, присваивая каждой переменной результаты успеваемости студентов по конкретному предмету. · Выберем в меню Analyze (Анализ) Data Reduction (Обработка данных) Factor (Факторный анализ). Появится диалоговое окно Factor Analysis (Факторный анализ) (рис. 2.9.1). · Переменные «социология», «информатика», «культорология», «математика» поместим в поле исследуемых переменных. · После чего, нажав кнопку Descriptives (Описание) в появившемся окне установим флажок напротив опции Coefficients (Коэффициенты), далее Continue (рис. 2.9.2). · Далее нажмем кнопку Rotation (Вращение), которая позволяет выбрать метод вращения. Активируем метод Варимакса, установив флажок напротив опции Varimax и оставим активированным вывод повёрнутой матрицы факторов (рис. 2.9.3). · Ничего больше не меняя, начнем расчёт нажатием ОК.
Рис. 2.9.1. Вид диалогового окна «Факторный анализ»
Рис. 2.9.2. Вид диалогового окна «Факторный анализ: Описание»
Рис. 2.9.3. Вид диалогового окна «Факторный анализ: Вращение» Вывод основных результатов, необходимых для дальнейших расчетов, выглядит следующим образом (рис. 2.9.4):
Матрица корреляций:
Повёрнутая матрица компонентов:
Объяснённая суммарная дисперсия
Рис. 2.9.4. Результат выполнения описанной процедуры Таким образом, видно, что матрица коэффициентов корреляции
При этом, если найти произведение
Видно, что выбранный один фактор не учитывает всю корреляцию (например, почти отсутствует корреляция между первым и третьим показателями), поэтому следует ввести в рассмотрение второй фактор, тогда матрица факторных нагрузок будет следующая:
Видно, что получившаяся матрица, с определенной погрешностью (связанной с остаточной корреляцией), отражает исходную матрицу коэффициентов корреляции. Попытаемся объяснить отобранные факторы. Имеющиеся 4 показателя можно описать двумя факторами. Фактор 1 наиболее полно характеризует первый и третий показатели, фактор 2 – второй и четвертый.
|







 и матрица факторных нагрузок
и матрица факторных нагрузок  , при влияющем одном факторе будут следующими:
, при влияющем одном факторе будут следующими:
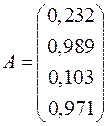
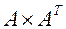 , то получим:
, то получим: