Выполнение. При построении линейной модели в качестве исследуемой переменной (зависимой) рассмотрим размер текущей з/п.
При построении линейной модели в качестве исследуемой переменной (зависимой) рассмотрим размер текущей з/п. Выберем в меню Analyze (Анализ) Regression (Регрессия) Linear (Линейная). Появится диалоговое окно (см. рис. 2.11.1).
Рис. 2.11.1. Диалоговое окно «Линейная регрессия»
Поместим переменную тек_з_п в поле для зависимых переменных, а остальные переменные в поле для независимых переменных. Для множественного анализа с несколькими независимыми переменными не рекомендуется оставлять метод включения всех переменных, установленный по умолчанию. Этот метод соответствует одновременной обработке всех независимых переменных, выбранных для анализа, и поэтому он может рекомендоваться для использования только в случае простого анализа с одной независимой переменной. Для множественного анализа следует выбрать один из пошаговых методов. При прямом методе независимые переменные, которые имеют наибольшие коэффициенты частной корреляции с зависимой переменной, пошагово увязываются в регрессионном уравнении. При обратном методе начинают с результата, содержащего все независимые переменные, и затем исключают независимые переменные с наименьшими частными корреляционными коэффициентами, пока соответствующий регрессионный коэффициент не оказывается незначимым (в данном случае уровень значимости равен 0,1). Наиболее распространенным является пошаговый метод, который устроен так же, как и прямой метод, однако после каждого шага переменные, используемые в данный момент, исследуются по обратному методу. При пошаговом методе могут задаваться блоки независимых переменных; в этом случае заданные блоки на одном шаге обрабатываются совместно. Выберем пошаговый метод, но воздержимся от блочной формы ввода данных, не задавая больше ни каких дополнительных расчётов, и начнем вычисление нажатием ОК.
Рис. 2.11.2. Результаты анализа «Сводка для модели»
Из таблицы «Сводка для модели» следует, что вовлечение переменных в расчет производилось за четыре шага, то есть переменные образование, начальная з/п, проработанное время, предшествующий опыт работников поочерёдно внедрялись в уравнение регрессии. Для каждого шага происходит вывод коэффициентов множественной регрессии, меры определённости, смещенной меры определённости и стандартной ошибки. К указанным результатам пошагово присоединяются результаты расчёта дисперсии, которые здесь не приводятся. Также, пошаговым образом, производится вывод соответствующих коэффициентов регрессии и значимость их отличия от нуля (рис. 2.11.3).
Рис. 2.11.3. Коэффициенты линейной модели
Уравнение регрессии для прогнозирования значения тек_з_п выглядит следующим образом: тек_з_п = 669,914 ×образование + 161,486 ×время_раб – 17,303 ×предшес_опыт + 1,768 ×нач_з_п При помощи соответствующих опций можно организовать вывод большого числа дополнительных статистических характеристик и графиков. Можно также создать много дополнительных переменных и добавить их в исходный файл данных.
Пример 2.11.2. Имеются 12 наблюдений за тремя показателями:
Используя пакет для обработки статистических данных получить уравнение множественной линейной регрессии и проанализировать качество полученной модели. Решение. Построим уравнение регрессии в виде
Создадим в пакете SPSS 13 файл с данными:
Выберем в меню пункты (опции) Analyze... (Анализ) Regression...(Регрессия) Linear... (Линейная). Появится диалоговое окно Linear Regression (Линейная регрессия) (рис.5.4). Перенесем переменную Y в поле для зависимых переменных и присвоим переменным x_1, x_2, x_3 статус независимых переменных. После нажатия кнопки «Statistics…» в появившемся окне установим флажки напротив опций «R squared change» и «Descriptives», далее нажимаем клавишу «Continue» (рис.5.5). Расчет параметров модели начинается нажатием клавиши ОК.
Вывод основных результатов выглядит следующим образом: Descriptive Statistics
Variables Entered/Removedb
a. All requested entered b. Dependent Variable: y Correlations
Model Summarry
a. Predictors: (Constant), x_3, x_1, x_2
ANOVAb
a. Predictors: (Constant), x_3, x_1, x_2 b. Depended Variable: y Coefficientsa
Основные числовые характеристики исследуемых показателей будут следующие:
Параметры модели регрессии представлены в таблице «Coefficients». Таким образом уравнение множественной регрессии имеет вид:
Для сравнения влияния каждой независимой переменной вычислим стандартизированные коэффициенты регрессии
Увеличение показателя Аналогично, увеличение Коэффициенты эластичности будут равны
Увеличение переменных Проверим значимость модели множественной регрессии по
где Коэффициент детерминации модели
Наблюдаемое значение критерия
Отметим, что вычисления в пакете SPSS 13 дают то же значение
По таблице
Так как Проверим на значимость коэффициенты Имеем
где
Вычислим дисперсию остатков модели по соотношению
Средняя ошибка (точность) модели
Тогда
По таблице квантилей
Так как Так как
|






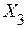

 .
.


 ;
;  ;
;  ;
;  ;
; ;
;  ;
;  ;
;  .
.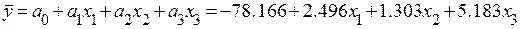 .
. ;
;  ;
;  .
. только на одно значение
только на одно значение  увеличивает в среднем показатель
увеличивает в среднем показатель  на
на  .
. на значение
на значение  увеличивает
увеличивает  . Увеличение
. Увеличение  на
на  увеличивает
увеличивает  .
. ;
; ;
; .
.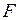 –критерию. Выдвигаем гипотезу
–критерию. Выдвигаем гипотезу  уравнение незначимо.
уравнение незначимо. ,
,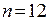 − количество наблюдений,
− количество наблюдений,  − количество показателей.
− количество показателей. .
. .
. .
. .
. , то есть все основания отвергнуть гипотезу
, то есть все основания отвергнуть гипотезу 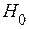 , то есть модель регрессии значима при уровне значимости
, то есть модель регрессии значима при уровне значимости 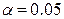 .
. ,
, 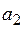 и
и 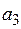 с помощью
с помощью  –критерия Стьюдента.
–критерия Стьюдента.

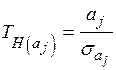 ,
, ,
,  − диагональные элемента матрицы
− диагональные элемента матрицы  .
.

 ;
;  ;
; ;
;  ;
; ;
;  .
.
 и
и  , то нет оснований отвергать гипотезу
, то нет оснований отвергать гипотезу  , то есть коэффициенты
, то есть коэффициенты  , то гипотезу
, то гипотезу  значим.
значим.


