Распознавание образов
Имеется матрица наблюдений Пусть исследователем указана принадлежность N 1 объектов к G образам, множествам, группам, классам, таксонам Число объектов, принадлежащих группе При этом Требуется найти принадлежность остальных N 2 = n – N 1 объектов к одному из указанных образов. Множества Существует большое число различных способов решения указанной задачи в зависимости от дополнительных свойств всего множества n объектов или его отдельных частей.
1. Байесовская теория принятия решения основана на минимизации общего риска принятия решения. Предполагается, что известна статистическая структура обучающих выборок, то есть вид распределения случайных величин, соответствующих каждому из образов. Если вид распределения неизвестен, то находят его оценку или вероятность появления объектов в каждой точке пространства. Пусть f (x | Sg), x О R m – oценка функции плотности распределения (ОФПР) для образа Sg. При условии равновероятного появления образов Sg объект с координатами x * следует отнести к тому образу, для которого f (x* | Sg) максимальнa. При различных вероятностях образов P (Sg) каждая из ОФПР домножается на некоторый коэффициент, зависящий от P (Sg).
2. Локальные методы распознавания учитывают расположение ближайших к х* точек ОВ и опираются на оценку
f (x* | Sg) = Mg /(ngV),
где V – объем некоторой окрестности точки; Mg – число объектов образа Sg, попавшего в этот объем. Например: а) правило "ближайшего соседа";– классифицируемый объект относится к тому образу, которому принадлежит ближайший объект из ОВ; б) "средняя связь"; – объект относится к той ОВ (образу), сумма расстояний до объектов которой меньше всего; в) "дальний сосед"; – объект относится к ОВ, расстояние до самого далекого объекта которой минимально.
|

 .
. .
.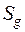 , известно и равно
, известно и равно 
 .
.


