Кластерный анализ
Рассматривается некоторая выборка наблюдаемых показателей
Задача состоит в классификации элементов выборки (объектов) по группам (классам, кластерам, таксонам, множествам) так, чтобы объекты внутри групп были схожими ("близкими" по соответствующим характеристикам), а сами группы были бы максимально различными (разделенными), насколько это возможно. Критерием классификации является некоторая функция "близости" или расстояние между объектами. Например, при классификации показателей характеристикой расстояния между
Другими примерами метрик близости являются: евклидово расстояние между показателями
расстояние между объектами
где Расстояние Хемминга между показателями определяется выражением: При конструировании различных кластер–процедур часто используется понятие расстояния не между отдельными объектами, а между целыми группами (классами, таксонами) объектов. 1. Расстояние между двумя группами Si и Sj равно расстоянию между ближайшими объектами этих групп (" ближайший сосед "):
2. Расстояние между двумя группами
Здесь 3. Расстояние между двумя группами
4. Расстояние между двумя группами
Здесь На практике иногда используются иерархические кластер–процедуры. Это пошаговый алгоритм, при котором на каждом шаге происходит разбиение (объединение) множества объектов, подлежащих классификации, на (в) непересекающиеся кластеры, при этом каждое последующее разбиение (объединение) относится к кластерам, полученным на предыдущем шаге. При работе таких процедур происходит построение так называемого иерархического классификационного дерева. Под ним понимается множество разбиений исходной выборки на классы, упорядоченные по уровням иерархии, т.е. по номеру шага иерархической процедуры. Из сказанного следует существование двух типов процедур: а) агломеративные, которые на каждом шаге объединяют полученные ранее кластеры в более крупные группы; б) дивизимные, которые на каждом шаге дробят полученные ранее кластеры на более мелкие. Примером агломеративной процедуры является пороговый алгоритм. Здесь имеется монотонно возрастающая последовательность порогов К недостаткам иерархических процедур относят громоздкость их реализации на ЭВМ. Достоинство – делают полный и достаточно тонкий анализ структуры объектов, например, при выявлении естественных групп признаков по алгоритму типа "средней связи" или "ближайшего соседа". Обнаружив такие группы можно снизить размерность описания либо выбрасыванием дублирующих (близких) признаков, либо заменив каждую группу новым показателем, общим для этой группы свойством с соответствующей интерпретацией. Общая схема иерархической процедуры (для определенности агломеративной): 1) все объекты считаются отдельными кластерами; 2) два самых близких кластера по матрице межклассовых расстояний объединяются в один; 3) пересчитывается матрица межклассовых расстояний; 4) переход к пункту 2. Очевидно такая процедура за n – 1 шагов (n – число объектов) объединит все объекты в один кластер. На каждом шаге будем фиксировать расстояние между объединяемыми кластерами как функцию j (t) от номера шага t. Такая функция будет монотонно возрастать, поскольку каждый раз происходит объединение ближайших классов, расстояние между которыми наименьшее (рис.3.8.1).
Рис.3.8.1. Принятие решения о классификации объектов
По производной j '(t) можно принять решение о том, что на шаге k – 1 была самая удачная группировка объектов, т.к. на шаге k были объединены кластеры (объекты) с большим межклассовым расстоянием (рис. 3.8.1). Дендограмма – графическое изображение результатов кластерного анализа в виде дерева решений.
|

 .
. и
и  часто является коэффициент корреляции
часто является коэффициент корреляции  , т.е. в этом случае функция "близости" или "расстояние" между
, т.е. в этом случае функция "близости" или "расстояние" между 
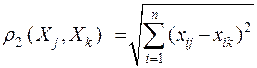 ;
; ,
, – вес j –го показателя.
– вес j –го показателя.

 и
и  равно расстоянию между их математическими ожиданиями (" центр тяжести ")
равно расстоянию между их математическими ожиданиями (" центр тяжести ")
 – вектор математического ожидания для i–й группы.
– вектор математического ожидания для i–й группы.

 – число объектов в группе
– число объектов в группе  и на каждом шаге t к одному классу относятся те объекты, расстояние между которыми не превосходит
и на каждом шаге t к одному классу относятся те объекты, расстояние между которыми не превосходит  .
.



