Метод главных компонент
В компонентном анализе вычисляются главные компоненты, т.е. некоррелированные комбинации исходных показателей, сохраняющие их общую дисперсию без изменений. Определение главных компонент (ГК) производится по корреляционной матрице исходных показателей. Результатом компонентного анализа на ЭВМ являются дисперсии главных компонент, их доли в общей дисперсии и сами главные компоненты. Другими словами, метод главных компонент (МГК) позволяет по заданной (вычисленной) m –мерной корреляционной матрице R исходных показателей Процедуру вычисления последовательностей осей можно прекратить в любом месте и, например, выбрать только две первые главные компоненты, которые воспроизводят, например, лишь 80% полной дисперсии. Главные компоненты представляют собой новое множество показателей До определения главных компонент следует центрировать и нормализовать исходные данные. Так как величины Переход осуществляется по формуле:
Для стандартизованных переменных легко вычисляются все основные числовые характеристики:
Каждый стандартизованный показатель имеет нулевое среднее значение, единичную дисперсию и безразмерен, что облегчает его интерпретацию. Пусть
Необходимо найти вектор–столбец Выражение для дисперсии можно переписать в эквивалентной форме в виде скалярного произведения
Решением этого соотношения является максимальное собственное значение матрицы Аналогично находятся остальные ГК. Таким образом, первые
процентов дисперсии исходных переменных. На практике обычно ограничиваются таким числом компонент, при котором При этом условии число ГК получается значительно меньшим числа исходных показателей, что облегчает процесс анализа данных. Коэффициенты
где Исходя из значений коэффициентов главных компонент можно ранжировать факторы по степени их значимости в главной компоненте. Можно вычислить индивидуальные значения главных компонент (для каждого наблюдения) и использовать их в дальнейшем для построения уравнения регрессии для исходных показателей.
|

 найти новую ортогональную m –мерную систему координат
найти новую ортогональную m –мерную систему координат  и именно так, чтобы максимум полной дисперсии лежал в направлении первой главной оси, а максимум оставшийся дисперсии – в направлении второй главной оси и т.д.
и именно так, чтобы максимум полной дисперсии лежал в направлении первой главной оси, а максимум оставшийся дисперсии – в направлении второй главной оси и т.д. .
.

 – корреляционная матрица стандартизованный показателей. Тогда, в соответствии с определением, дисперсия вектора
– корреляционная матрица стандартизованный показателей. Тогда, в соответствии с определением, дисперсия вектора  равна
равна
 , который максимизирует эту дисперсию при условии
, который максимизирует эту дисперсию при условии  которое обеспечивает единственность решения.
которое обеспечивает единственность решения.
 .
. главных компонент объясняют
главных компонент объясняют
 .
. главных компонент определяются по формуле
главных компонент определяются по формуле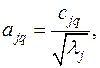
 – максимальное собственное значение матрицы и соответствующий ему собственный вектор применительно к j –й ГК.
– максимальное собственное значение матрицы и соответствующий ему собственный вектор применительно к j –й ГК.


