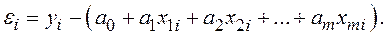Проверка значимости и качества модели регрессииЗначимость уравнения регрессии в целом сводится к проверке гипотезы об одновременном равенстве нулю всех коэффициентов регрессии при независимых переменных: Для проверки значимости модели регрессии используется F –критерий Фишера:
где п – число наблюдений; m – число независимых переменных, включенных в модель. Если расчетное значение Для оценки качества модели множественной регрессии часто вычисляют коэффициент множественной корреляции (индекс корреляции) R и коэффициент детерминации R 2. В многофакторной регрессии добавление дополнительных объясняющих переменных увеличивает коэффициент детерминации. Следовательно, коэффициент детерминации должен быть скорректирован с учетом числа независимых переменных. Скорректированный (нормированный) коэффициент детерминации
где п – число наблюдений; m – число независимых переменных. В целом качество модели оценивается стандартным для математических моделей образом: по адекватности и точности на основе анализа остатков регрессии
Расчетные значения результирующего показателя получаются путем подстановки в модель фактических значений всех включенных факторов.
|
,
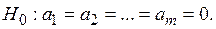
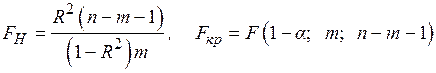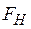больше табличного (критического) значения при заданном уровне значимости 
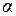, то модель считается значимой (адекватной имеющимся наблюдениям).
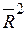рассчитывается по соотношению:
,
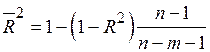