Оценка качества линейного уравнения парной регрессии
Для оценки качества парной линейной регрессионной модели целесообразно: 1) вычислить и оценить значимость коэффициента корреляции; 2) проверить адекватность (значимость) всей модели регрессии; 3) оценить среднее квадратическое отклонение остатков 4) проверить значимость параметров а и b модели регрессии; 5) определить доверительные границы модели регрессии; 6) определить интервальные оценки параметров а и b модели регрессии. Для проверки значимости модели парной линейной регрессии используется F –критерий Фишера:
В качестве меры точности парной линейной регрессии применяют стандартную ошибку
С помощью величины Проведем анализ значимости параметров модели парной линейной регрессии Наблюдаемые значения По данным выборки эти отклонения и соответственно их дисперсия не оцениваются, а используются отклонения зависимой переменной
Так как предполагается, что ошибки (остатки) ei нормально распределены, то среднеквадратическое отклонение ошибок используется для измерения вариации параметров регрессионной модели. Среднеквадратические отклонения коэффициентов определяются по формулам:
где Проверка значимости отдельных коэффициентов регрессии связана с определением наблюдаемых (расчетных) значений Т –критерия (Т –статистики) для соответствующих коэффициентов регрессии. Нулевая (проверяемая) гипотеза в данном случае имеет вид: Наблюдаемые значения критерия
Если расчетное значение критерия В противном случае фактор, соответствующий этому коэффициенту, следует исключить из модели (при этом ее качество не ухудшится). Для значимого уравнения регрессии представляет интерес построение интервальных оценок для параметра b и свободного члена а
где
|

 ;
; .
.
 можно построить доверительные границы для уравнения регрессии.
можно построить доверительные границы для уравнения регрессии.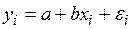 .
.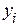 , соответствующие данным
, соответствующие данным  , являются случайными. Случайными являются и рассчитанные по ним значения коэффициентов а и b. Надежность получаемых оценок а и b зависит от дисперсии случайных отклонений (ошибок).
, являются случайными. Случайными являются и рассчитанные по ним значения коэффициентов а и b. Надежность получаемых оценок а и b зависит от дисперсии случайных отклонений (ошибок). :
: .
.

 – оценка математического ожидания (среднее значение) независимой переменной Х;
– оценка математического ожидания (среднее значение) независимой переменной Х; 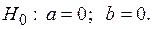
 и
и  сравниваются с табличными (при двухсторонней критической области)
сравниваются с табличными (при двухсторонней критической области)
 превосходит его табличное значение
превосходит его табличное значение  при заданном уровне значимости a (0.1; 0.05; 0.01), коэффициент регрессии считается значимым.
при заданном уровне значимости a (0.1; 0.05; 0.01), коэффициент регрессии считается значимым.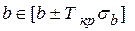 ;
;  ,
,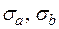 – стандартные отклонения свободного члена и коэффициента регрессии соответственно; n – число наблюдений.
– стандартные отклонения свободного члена и коэффициента регрессии соответственно; n – число наблюдений.


