Нелинейная парная регрессия
Если между результативным и факторным признаком существует нелинейная зависимость, то она выражается с помощью соответствующих нелинейных функций. Для описания нелинейной связи между 1) параболическая 2) кубическая парабола 4) гиперболическая 5) логарифмическая 6) степенная 7) показательная 8) экспоненциальная 9) логистическая и некоторые другие. Здесь Различают 2 класса нелинейных регрессионных моделей: 1) регрессии, нелинейные относительно переменных, но линейные по параметрам (полиномы разных степеней, гипербола и др.); 2) регрессии, нелинейные по оцениваемым параметрам (степенная, показательная, экспоненциальная и др.). Если коэффициенты регрессии входят в регрессионную модель линейно, то метод наименьших квадратов приводит к системе линейных алгебраических уравнений относительно искомых коэффициентов. В противном случае – к нелинейной системе уравнений. Так в случае выбора теоретической функции в виде полинома k –й степени (функция линейна относительно параметров), исходя из критерия метода наименьших квадратов
(вычисляя и приравнивая нулю частные производные
Решая эту систему, найдем неизвестные параметры В случае параболической регрессионной модели коэффициенты регрессии определяются из системы линейных уравнений
Если в качестве теоретической функции выбрана гиперболическая функция, то параметры регрессии определяются из линейной системы
Если модель нелинейна относительно параметров регрессии, то она в ряде случаев с помощью соответствующих преобразований может быть приведена к линейному виду. Если же модель не может быть приведена к линейному виду, то для оценки параметров в этом случае приходиться решать системы нелинейных уравнений, используя итерационные методы. В этом случае успех в нахождении параметров регрессии зависит от сложности полученной системы.
|

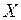 и
и  используют следующие виды функций:
используют следующие виды функций: ;
; ;
; ;
; ;
; ;
;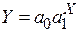 ;
; ;
;
 – неизвестные параметры (коэффициенты регрессии), подлежащие определению. Необходимо подобрать значения этих параметров, обеспечивающие наилучшее приближение теоретической функцией эмпирических данных.
– неизвестные параметры (коэффициенты регрессии), подлежащие определению. Необходимо подобрать значения этих параметров, обеспечивающие наилучшее приближение теоретической функцией эмпирических данных.
 ,
,  ), получим линейную систему уравнений
), получим линейную систему уравнений
 .
.




