Регрессионный анализ
Между результативным и факторными показателями может существовать функциональная связь, которая характеризуются полным соответствием между изменением факторных признаков и изменением результативной величины, то есть каждому конкретному набору значений факторов соответствует определенное значение результативного признака. Например, при повременной оплате труда размер зарплаты функциональ–но зависит от количества отработанного времени. Связь между причинами и следствием многозначна и часто носит вероятностный характер. В данном случае имеем стохастическую зависимость (рис. 3.3.1). Стохастическая связь состоит в том, что одна величина (показатель) реагирует на изменение другой изменением своего закона распределения. Частный случай стохастической связи – статистическая связь (корреляционная).
Рис.3.3.1. Построение стохастической связи двух переменных
Частный случай стохастической связи – статистическая связь (корреляционная). Пусть исследуется некоторый экономический показатель Полагаем, что каждому набору значений факторов соответствует определенное значение Целью регрессионного анализа является установление функциональной зависимости
Уравнение регрессии называют еще регрессионной моделью. Одной из проблем построения уравнения регрессии является ее размерность, то есть определение числа факторов, включаемых в регрессионную модель. Сокращение числа факторов, включаемых в уравнение регрессии, позволяет получить более простую и легко реализуемую модель. В то же время модель малой размерности может привести к тому, что она будет недостаточно точно описывать исследуемое явление или процесс. Практика выработала критерий, позволяющий установить оптимальное соотношение между числом факторов и объемом исследуемой совокупности: число факторов должно быть в 5–6 раз меньше объема изучаемой совокупности. Регрессионный анализ включает следующие этапы: 1) определение вида функции, описывающей функциональную связь между результативным признаком и факторными признаками; 2) определение коэффициентов регрессии, то есть числовых параметров, входящих в уравнение регрессии; 3) расчет теоретических значений результативного признака для отдельных наборов значений факторов; 4) исследование отклонений расчетных значений от эмпирических данных; 5) оценка качества полученной модели и проверка соответствующих статистических гипотез о регрессии. В зависимости от вида функции В зависимости от количества включенных в модель факторов Отметим, что выбор вида теоретической функции После получения уравнения регрессии производится оценка его качества. Для оценки качества регрессионных моделей целесообразно: 1) вычислить и оценить значимость соответствующего параметра корреляционного анализа (линейного коэффициента корреляции для парной регрессии, коэффициента множественной корреляции, индекса корреляции и др.); 2) проверить адекватность (значимость) всей модели регрессии; 3) оценить точность модели, то есть вычислить среднее квадратическое отклонение остатков 4) проверить значимость каждого параметра модели регрессии; 5) определить доверительные границы всей модели регрессии; 6) определить доверительные границы (интервальные оценки) каждого параметра модели регрессии. Качество модели обычно оценивается стандартным образом: по адекватности и точности на основе анализа остатков регрессии
Расчетные значения получаются путем подстановки в модель фактических значений всех включенных факторов. Анализ остатков позволяет получить представление, насколько хорошо подобрана сама модель и насколько правильно выбран метод оценки коэффициентов. Оценка качества регрессионных моделей часто производится с использованием коэффициента детерминации R 2 (квадрат коэффициента множественной корреляции, индекса корреляции, линейного коэффициента корреляции). Коэффициент детерминации показывает долю вариации (дисперсии) результативного признака, находящегося под воздействием изучаемых факторов, то есть определяет, какая доля дисперсии признака Y учтена в модели и обусловлена влиянием на него других факторов. Чем ближе R 2 к 1, тем лучше качество модели. Оценить значимость всего уравнения регрессии – это означает установить, соответствует ли математическая модель, выражающая зависимость между Для проверки значимости модели регрессии используется F –критерий Фишера с использованием коэффициента детерминации:
где
Если расчетное значение В качестве меры точности применяют несмещенную оценку дисперсии остаточной компоненты, которая представляет собой отношение суммы квадратов уровней остаточной компоненты к числу степеней свободы, то есть к величине ( Квадратный корень из этой величины
Регрессионные модели могут быть использованы для прогнозирования возможных значений зависимой переменной. Прогнозируемое значение результативного показателя получается при подстановке в уравнение регрессии соответствующих значений факторов. Такой прогноз называется точечным. При этом в уравнение регрессии нельзя подставлять такие значения факторов, которые значительно отличаются от значений факторов, входящих в исследуемую выборку, на основе которой получено уравнение регрессии. Вероятность реализации точечного прогноза практически равна нулю. Поэтому рассчитывается средняя ошибка прогноза или доверительный интервал прогноза с достаточно большой вероятностью (надежностью). Для парной регрессии доверительный интервал всей линии регрессии определяется соотношением:
где При этом стандартная ошибка линии регрессии определяется соотношением
Рис.3.3.2. Доверительные границы для уравнения регрессии
Доверительный интервал для прогнозов индивидуальных значений
где Расположение границ доверительного интервала показывает, что прогноз значений зависимой переменной по уравнению регрессии удовлетворителен только в случае, если значение фактора В противном случае экстраполяция по уравнению регрессии может дать значительную погрешность.
|


 (результативный признак). Установлено, что на него воздействуют факторы
(результативный признак). Установлено, что на него воздействуют факторы 
 .
. соответствует значение результативного признака, равное
соответствует значение результативного признака, равное  (
( ).
). .
. модели делятся на линейные и нелинейные.
модели делятся на линейные и нелинейные. модели делятся на однофакторные (парная модель регрессии) и многофакторные (модель множественной регрессии).
модели делятся на однофакторные (парная модель регрессии) и многофакторные (модель множественной регрессии). для регрессионной модели может производиться на основе анализа эмпирических данных или путем рассмотрения нескольких функций с последующим выбором наилучшей по некоторому критерию.
для регрессионной модели может производиться на основе анализа эмпирических данных или путем рассмотрения нескольких функций с последующим выбором наилучшей по некоторому критерию. ;
;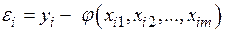 .
. для описания зависимой переменной Y.
для описания зависимой переменной Y. ,
,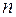 – число наблюдений;
– число наблюдений; – количество независимых факторов
– количество независимых факторов 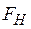 больше табличного (критического) значения
больше табличного (критического) значения  с
с  и
и 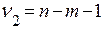 степенями свободы при заданном уровне значимости
степенями свободы при заданном уровне значимости 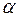 , то модель считается значимой.
, то модель считается значимой. ).
). называется стандартной ошибкой оценки:
называется стандартной ошибкой оценки: .
. ,
, – значение фактора
– значение фактора 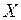 при котором вычисляется прогнозное значение результативного показателя (рис. 5.2).
при котором вычисляется прогнозное значение результативного показателя (рис. 5.2).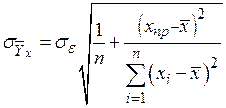 .
.
 определяется из соотношения:
определяется из соотношения: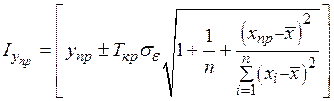 ,
, – прогнозное значение фактора
– прогнозное значение фактора 


