Множественная регрессия. Построение функциональной связи между результирующим показателем и двумя и более факторами носит название множественной (многофакторнойПостроение функциональной связи между результирующим показателем и двумя и более факторами носит название множественной (многофакторной, многомерной) регрессии. При этом уравнение регрессии имеет вид
В случае множественной регрессии выбор формы связи оказывается значительно более сложным по сравнению с парной регрессией. Практика построения многофакторных моделей показывает, что реально существующие в экономике зависимости можно описать, используя следующие типы моделей: 1) линейная 2) степенная 3) экспоненциальная 4) параболическая 5) гиперболическая Основное значение имеют линейные модели (относительно параметров регрессии) в силу своей простоты. Нелинейные формы зависимости часто преобразуются к линейным путем линеаризации. Наиболее приемлемым способом определения вида уравнения регрессии является метод перебора различных уравнений регрессии. Наилучшие значения параметров регрессии Коэффициенты регрессии находятся по критерию:
где Реализация этого критерия приводит к системе уравнений
из которой определяются
|
.
;
;
;
;
.
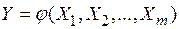определяются методом наименьших квадратов.
,
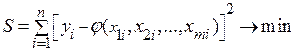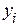– значение результативного фактора (зависимой переменной) 
в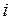 
–ом наблюдении; 
– значения факторов 
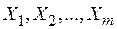в 
– количество наблюдений.
,
