Правило сложения дисперсий
В статистическом исследовании очень часто бывает необходимо не только изучить вариации признака по всей совокупности, но и проследить количественные изменения признака по однородным группам совокупности, а также и между группами. Следовательно, помимо общей средней для всей совокупности необходимо просчитывать и частные средние величины по отдельным группам. Различают следующие виды дисперсии. Общая дисперсия измеряет всю вариацию признака под влиянием всех факторов (3):
Межгрупповая дисперсия характеризует систематическую вариацию, т.е. различия в величине изучаемого признака, возникающие под влиянием признака – фактора, положенного в основании группировки (4).
где Внутригрупповая дисперсия отражает случайную вариацию, т.е. часть вариации, происходящую под влиянием неучтенных факторов. Данная дисперсия рассчитывается отдельно для каждой группы по формуле (5). Далее вычисляется средняя из внутригрупповых дисперсий, как средневзвешенная величина с учетом частоты каждой группы (5).
Согласно правилу сложения дисперсий, общая дисперсия, возникающая под влиянием всех факторов, равна сумме дисперсий, возникающих под влиянием случайных факторов и дисперсии, возникающей за счет группировочного фактора (6).
В SPSS дисперсионный анализ реализуется следующим образом. Analyze (Анализ) / Compare Means One-Way-ANOVA (рис.22) Откроется диалоговое окно дисперсионного анализа.
Рис. 22. Вид окна запуска дисперсионного анализа
Таблица 9.
|

 (3)
(3)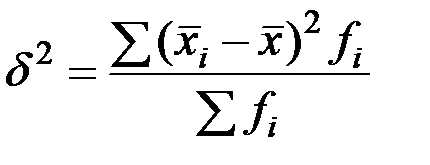 (4),
(4), - средняя i – той группы,
- средняя i – той группы,  - общая средняя признака x,
- общая средняя признака x,  - частота i-той группы.
- частота i-той группы. (5)
(5) (6)
(6)



