Вычисление площадей плоских фигур 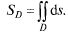
Пример: 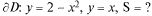
Определим точки пересечения кривых: х-2- 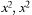 + х - 2 = О,
+ х - 2 = О,
 = -2;1;
= -2;1;  (-2,-2),
(-2,-2),  (1, 1) (рис. 23.9).
(1, 1) (рис. 23.9).
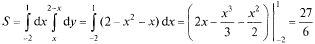
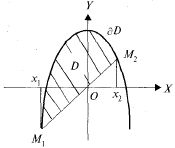
Рис. 23.9
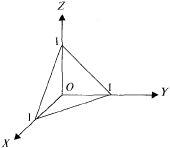
Рис. 23.10
Вычисление объемов цилиндрических тел
 (см. разд. 23.1).
(см. разд. 23.1).
Пример: 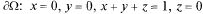 (рис. 23.11). V =?
(рис. 23.11). V =?

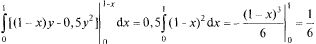
Замечание. Если тело, объем которого нужно найти, ограничено сверху поверхностью 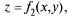 а снизу
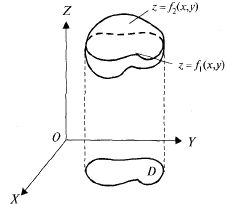
а снизу  причем проекцией обеих поверхностей на плоскость XOY является область D, то объем V этого тела (рис. 23.11) вычисляется по формуле
причем проекцией обеих поверхностей на плоскость XOY является область D, то объем V этого тела (рис. 23.11) вычисляется по формуле
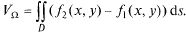
| ОПРЕДЕЛЕНИЕ ТРОЙНОГО ИНТЕГРАЛА
|
|
Пусть задана область V Ì XOYZ, ограниченная замкнутой поверхностью; в области V и на ее границе задана функция f (x, y, z).
| 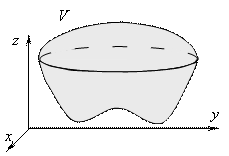
| Тройным интегралом от функции f(x, y, z ) по области V называется конечный предел трехмерной интегральной суммы при стремлении к нулю ранга разбиения, порождающего эту сумму (если этот предел существует и не зависит ни от способа разбиения области V на элементарные части, ни от выбора точек на каждой из этих элементарных частей):

здесь n – это количество элементарных частей разбиения области V;
Pi (xi, yi, zi) – произвольно выбранная точка на каждой элементарной части,
i = 1,..., n;
 — ранг разбиения; — ранг разбиения;
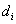 – диаметр i -ой элементарной части. – диаметр i -ой элементарной части.
|
Достаточное условие существования тройного интеграла
Если функция f (x, y, z) непрерывная в замкнутой области V, то  существует.
существует.

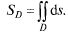
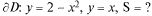
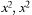 + х - 2 = О,
+ х - 2 = О, = -2;1;
= -2;1;  (-2,-2),
(-2,-2),  (1, 1) (рис. 23.9).
(1, 1) (рис. 23.9).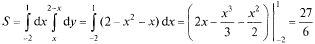


 (см. разд. 23.1).
(см. разд. 23.1).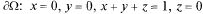 (рис. 23.11). V =?
(рис. 23.11). V =?
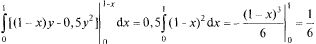
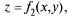 а снизу
а снизу  причем проекцией обеих поверхностей на плоскость XOY является область D, то объем V этого тела (рис. 23.11) вычисляется по формуле
причем проекцией обеих поверхностей на плоскость XOY является область D, то объем V этого тела (рис. 23.11) вычисляется по формуле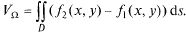



 — ранг разбиения;
— ранг разбиения;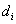 – диаметр i -ой элементарной части.
– диаметр i -ой элементарной части. существует.
существует.


