Вычисление тройного интеграла сводится к вычислению трехкратного интеграла.

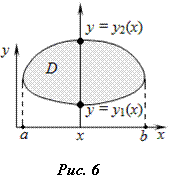
В декартовых координатах область V, правильная в направлении оси OZ, записывается системой неравенств
 ,
,
где D – это проекция области V на плоскость XOY, а поверхности  и
и  ограничивают область V соответственно снизу и сверху (Рис. 6).
ограничивают область V соответственно снизу и сверху (Рис. 6).
Если двумерную область D также записать системой неравенств  , то трехмерная область V запишется системой трех неравенств
, то трехмерная область V запишется системой трех неравенств 
Тогда тройной интеграл сводится сначала к двойному, а затем к трёхкратному с учётом того, что в декартовых координатах dV = dx × dy × dz;
формула сведения тройного интеграла к трехкратному интегралу имеет следующий вид:

| (1)
|
Существует всего 6 вариантов сведения тройного интеграла к трехкратному в декартовых координатах (в зависимости от выбранного порядка интегрирования).
Пример 1 (вычисление тройного интеграла в декартовых координатах)
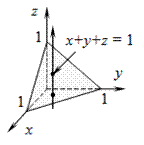
Вычислить  , где область V ограничена поверхностями
, где область V ограничена поверхностями  .
.
Решение
| 
|
Запишем область V системой трёх неравенств:

|
Сводим тройной интеграл к трехкратному по формуле (1) в соответствии с системой
неравенств и вычисляем трехкратный интеграл:




 .
.
| Замена переменных в тройных интегралах
| | | При вычислении тройного интеграла, как и двойного, часто удобно сделать замену переменных. Это позволяет упростить вид области интегрирования или подынтегральное выражение. Пусть исходный тройной интеграл задан в декартовых координатах x, y, z в области U:
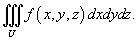 Требуется вычислить данный интеграл в новых координатах u, v, w. Взаимосвязь старых и новых координат описывается соотношениями:
Требуется вычислить данный интеграл в новых координатах u, v, w. Взаимосвязь старых и новых координат описывается соотношениями:
 Предполагается, что выполнены следующие условия:
1. Функции φ, ψ, χ непрерывны вместе со своими частными производными;
2. Существует взаимно-однозначное соответствие между точками области интегрирования U в пространстве xyz и точками области U' в пространстве uvw;
3. Якобиан преобразования I (u,v,w), равный
Предполагается, что выполнены следующие условия:
1. Функции φ, ψ, χ непрерывны вместе со своими частными производными;
2. Существует взаимно-однозначное соответствие между точками области интегрирования U в пространстве xyz и точками области U' в пространстве uvw;
3. Якобиан преобразования I (u,v,w), равный
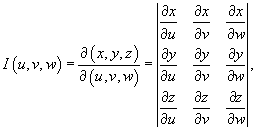 отличен от нуля и сохраняет постоянный знак всюду в области интегрирования U.
Тогда формула замены переменных в тройном интеграле записывается в виде:
отличен от нуля и сохраняет постоянный знак всюду в области интегрирования U.
Тогда формула замены переменных в тройном интеграле записывается в виде:
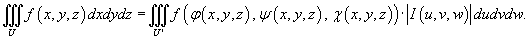
| |
| Тройные интегралы в сферических координатах
|
| |
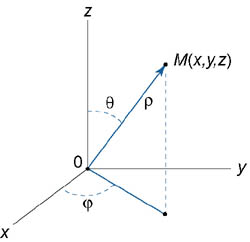
Сферическими координатами точки M (x,y,z) называются три числа − ρ, φ, θ, где
ρ − длина радиуса-вектора точки M; φ − угол, образованный проекцией радиуса-вектора  на плоскость Oxy и осью Ox; θ − угол отклонения радиуса-вектора на плоскость Oxy и осью Ox; θ − угол отклонения радиуса-вектора  от положительного направления оси Oz (рисунок 1). от положительного направления оси Oz (рисунок 1).
| | | | Рис.1
| | | Обратите внимание, что определения ρ, φ в сферических и цилиндрических координатах отличаются друг от друга.
Сферические координаты точки связаны с ее декартовыми координатами соотношениями
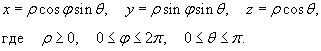
Якобиан перехода от декартовых координат к сферическим имеет вид:
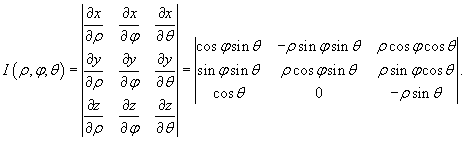
Раскладывая определитель по второму столбцу, получаем
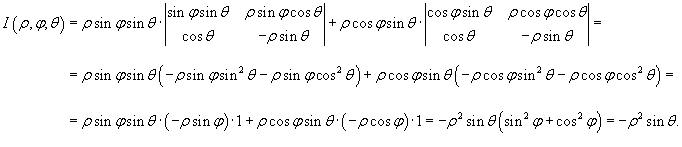
Соответственно, абсолютное значение якобиана равно
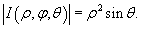
Следовательно, формула замены переменных при преобразовании декартовых координат в сферические имеет вид:
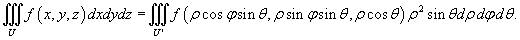
Тройной интеграл удобнее вычислять в сферических координатах, когда область интегрирования U представляет собой шар (или некоторую его часть) и/или когда подынтегральное выражение имеет вид f (x 2 + y 2 + z 2).
Иногда выгодно использовать т.н. обощенные сферические координаты, связанные с декартовыми формулами
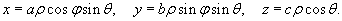
В этом случае якобиан равен
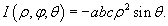
|
| Криволинейные интегралы первого рода
|
| |
Определение
Пусть кривая C описывается векторной функцией  , где переменная s представляет собой длину дуги кривой (рисунок 1). Если на кривой C определена скалярная функция F, то интеграл , где переменная s представляет собой длину дуги кривой (рисунок 1). Если на кривой C определена скалярная функция F, то интеграл  называется криволинейным интегралом первого рода от скалярной функции F вдоль кривой C и обозначается как называется криволинейным интегралом первого рода от скалярной функции F вдоль кривой C и обозначается как
 Криволинейный интеграл
Криволинейный интеграл  существует, если функция F непрерывна на кривой C. существует, если функция F непрерывна на кривой C.

| | 
| | Рис.1
| | Рис.2
| |



 ,
, и
и  ограничивают область V соответственно снизу и сверху (Рис. 6).
ограничивают область V соответственно снизу и сверху (Рис. 6). , то трехмерная область V запишется системой трех неравенств
, то трехмерная область V запишется системой трех неравенств 

 , где область V ограничена поверхностями
, где область V ограничена поверхностями  .
.






 .
.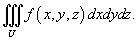 Требуется вычислить данный интеграл в новых координатах u, v, w. Взаимосвязь старых и новых координат описывается соотношениями:
Требуется вычислить данный интеграл в новых координатах u, v, w. Взаимосвязь старых и новых координат описывается соотношениями:
 Предполагается, что выполнены следующие условия:
1. Функции φ, ψ, χ непрерывны вместе со своими частными производными;
2. Существует взаимно-однозначное соответствие между точками области интегрирования U в пространстве xyz и точками области U' в пространстве uvw;
3. Якобиан преобразования I (u,v,w), равный
Предполагается, что выполнены следующие условия:
1. Функции φ, ψ, χ непрерывны вместе со своими частными производными;
2. Существует взаимно-однозначное соответствие между точками области интегрирования U в пространстве xyz и точками области U' в пространстве uvw;
3. Якобиан преобразования I (u,v,w), равный
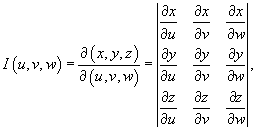 отличен от нуля и сохраняет постоянный знак всюду в области интегрирования U.
Тогда формула замены переменных в тройном интеграле записывается в виде:
отличен от нуля и сохраняет постоянный знак всюду в области интегрирования U.
Тогда формула замены переменных в тройном интеграле записывается в виде:
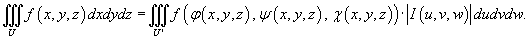
 на плоскость Oxy и осью Ox; θ − угол отклонения радиуса-вектора
на плоскость Oxy и осью Ox; θ − угол отклонения радиуса-вектора 
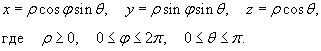
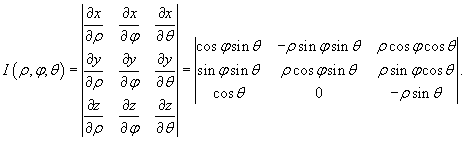
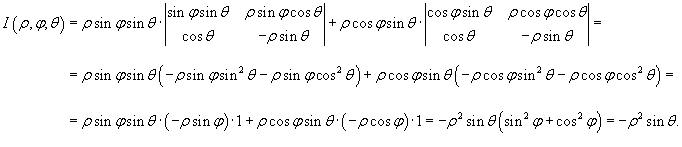
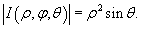
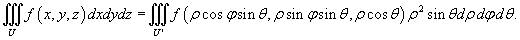
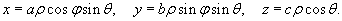
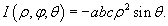
 , где переменная s представляет собой длину дуги кривой (рисунок 1). Если на кривой C определена скалярная функция F, то интеграл
, где переменная s представляет собой длину дуги кривой (рисунок 1). Если на кривой C определена скалярная функция F, то интеграл  называется криволинейным интегралом первого рода от скалярной функции F вдоль кривой C и обозначается как
называется криволинейным интегралом первого рода от скалярной функции F вдоль кривой C и обозначается как
 Криволинейный интеграл
Криволинейный интеграл  существует, если функция F непрерывна на кривой C.
существует, если функция F непрерывна на кривой C.





