Пусть функции P(x,y), Q(x,y), P'y(х,у), Q'x(х,у) непрерывны в замкнутой области D, ограниченной контуром L (рис. 3.6). 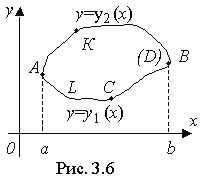
Пусть контур L, кроме того, пересекается прямыми, параллельными осям координат, не более чем в двух точках.
Пусть уравнение АСВ есть y = y1(x) при a ≤ x ≤ b, и уравнение АКВ есть y = y2(x) при a ≤ x ≤ b.
Преобразуем двойной интеграл:

здесь символ  означает криволинейный интеграл по замкнутому контуру L.
означает криволинейный интеграл по замкнутому контуру L.
Аналогично получается
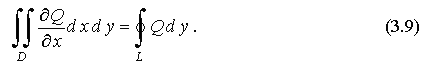
Вычитая из формулы (3.9) формулу (3.8), получаем формулу Грина
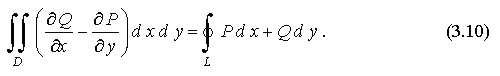
| Независимость криволинейных интегралов от пути интегрирования
|
| |
Определения
Криволинейный интеграл второго рода от векторной функции  не зависит от пути интегрирования, если P, Q и R являются непрерывными функциями в области интегрирования D и в этой области существует скалярная функция не зависит от пути интегрирования, если P, Q и R являются непрерывными функциями в области интегрирования D и в этой области существует скалярная функция  , такая, что , такая, что
 В этом случае криволинейный интеграл второго рода от функции
В этом случае криволинейный интеграл второго рода от функции  вдоль кривой C от точки A до точки B выражается формулой вдоль кривой C от точки A до точки B выражается формулой
 (Здесь можно увидеть аналогию с формулой Ньютона-Лейбница для определенных интегралов.) Таким образом, если криволинейный интеграл не зависит от пути интегрирования, то для любого замкнутого контура C справедливо соотношение
(Здесь можно увидеть аналогию с формулой Ньютона-Лейбница для определенных интегралов.) Таким образом, если криволинейный интеграл не зависит от пути интегрирования, то для любого замкнутого контура C справедливо соотношение
 Векторное поле, обладающее свойством
Векторное поле, обладающее свойством  , называется потенциальным, а функция , называется потенциальным, а функция  называется потенциалом.
Признак потенциальности поля
Криволинейный интеграл II рода от функции называется потенциалом.
Признак потенциальности поля
Криволинейный интеграл II рода от функции  не зависит от пути интегрирования, если не зависит от пути интегрирования, если
 Предполагается, что каждый компонент функции
Предполагается, что каждый компонент функции  имеет непрерывные частные производные по переменным x, y и z. Если криволинейный интеграл рассматривается в плоскости O xy, то в случае потенциального поля будет справедливо соотношение имеет непрерывные частные производные по переменным x, y и z. Если криволинейный интеграл рассматривается в плоскости O xy, то в случае потенциального поля будет справедливо соотношение
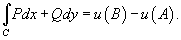 В этом случае признак потенциальности векторного поля упрощается и принимает вид
В этом случае признак потенциальности векторного поля упрощается и принимает вид
 Рассмотренный признак является необходимым, но, вообще говоря, не достаточным для потенциальности поля. Данное условие достаточно, если только область интегрирования D односвязна.
Рассмотренный признак является необходимым, но, вообще говоря, не достаточным для потенциальности поля. Данное условие достаточно, если только область интегрирования D односвязна.
|



 означает криволинейный интеграл по замкнутому контуру L.
означает криволинейный интеграл по замкнутому контуру L.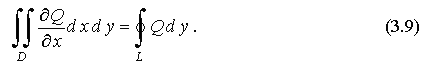
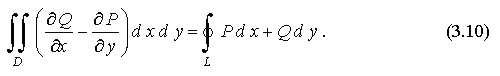
 не зависит от пути интегрирования, если P, Q и R являются непрерывными функциями в области интегрирования D и в этой области существует скалярная функция
не зависит от пути интегрирования, если P, Q и R являются непрерывными функциями в области интегрирования D и в этой области существует скалярная функция  , такая, что
, такая, что
 В этом случае криволинейный интеграл второго рода от функции
В этом случае криволинейный интеграл второго рода от функции  вдоль кривой C от точки A до точки B выражается формулой
вдоль кривой C от точки A до точки B выражается формулой
 (Здесь можно увидеть аналогию с формулой Ньютона-Лейбница для определенных интегралов.) Таким образом, если криволинейный интеграл не зависит от пути интегрирования, то для любого замкнутого контура C справедливо соотношение
(Здесь можно увидеть аналогию с формулой Ньютона-Лейбница для определенных интегралов.) Таким образом, если криволинейный интеграл не зависит от пути интегрирования, то для любого замкнутого контура C справедливо соотношение
 Векторное поле, обладающее свойством
Векторное поле, обладающее свойством  , называется потенциальным, а функция
, называется потенциальным, а функция  Предполагается, что каждый компонент функции
Предполагается, что каждый компонент функции 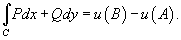 В этом случае признак потенциальности векторного поля упрощается и принимает вид
В этом случае признак потенциальности векторного поля упрощается и принимает вид
 Рассмотренный признак является необходимым, но, вообще говоря, не достаточным для потенциальности поля. Данное условие достаточно, если только область интегрирования D односвязна.
Рассмотренный признак является необходимым, но, вообще говоря, не достаточным для потенциальности поля. Данное условие достаточно, если только область интегрирования D односвязна.



