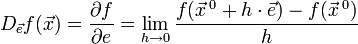Предположим, что выражение  есть полный дифференциал функции
есть полный дифференциал функции  . В соответствии с доказательствами условий независимости криволинейного интеграла
. В соответствии с доказательствами условий независимости криволинейного интеграла  от выбора пути
от выбора пути  можно заключить, что большое количество функций, которые удовлетворяют условию
можно заключить, что большое количество функций, которые удовлетворяют условию 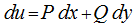 представляют собой
представляют собой
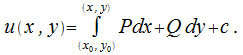
Для того, чтобы определить функцию  , за путь интегрирования можно принять, допустим,
, за путь интегрирования можно принять, допустим,  , здесь
, здесь  и
и  представлены в качестве отрезков, которые являются параллельными осям координат (рис. 26.7). В этом случае
представлены в качестве отрезков, которые являются параллельными осям координат (рис. 26.7). В этом случае
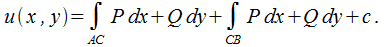
Учитывая то, что
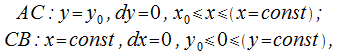
имеем
(26.6)
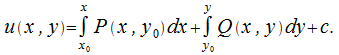
Пример 1: Определить, можно ли назвать выражение  полным дифференциалом
полным дифференциалом  Если это так, то вычислить
Если это так, то вычислить 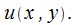
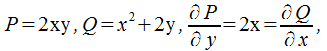
cледовательно,  В соответствии с (26.5) запишем
В соответствии с (26.5) запишем
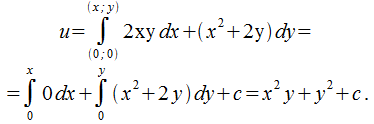
Пример 2: Найти 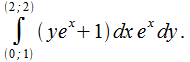
Выражение под знаком интеграла есть полный дифференциал  (рис.26.8). В этом случае
(рис.26.8). В этом случае  :
: 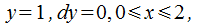
 :
: 
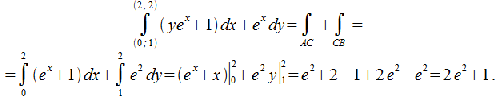

Рис. 26.7
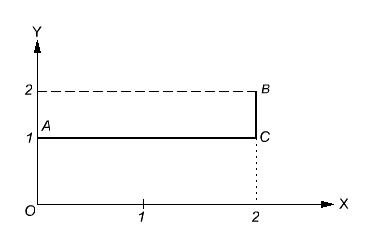
Рис. 26. 8
| 3.14. Скалярное поле, производная скалярной функции по заданному направлению
|
|
Будем вести рассмотрение этих новых понятий в двух или трёхмерном пространстве из-за простоты геометрической или физической интерпретаций.
Полем величины U называют область D трехмерного пространства, с каждой точкой M(x,y,z) которой в каждый момент времени t связано определённое значение величины "U".
Если U есть скалярная (векторная) величина, то и порождаемое ею поле называют скалярным (векторным). Задание скалярного поля есть задание скалярной функции U = f(M,t) = f(x,y,z).
Если величина U не зависит от времени t, то поле называют стационарным, или установившимся.
Пусть задано скалярное стационарное поле U = f(M) = f(x,y,z), где функцию f(x,y,z) будем всегда предполагать непрерывно дифференцируемой в рассматриваемой области.
Основной вопрос исследования скалярного поля есть вопрос об изменении функции U при переходе из одной точки пространства в другую. Для выяснения этого вопроса рассмотрим, прежде всего, геометрическое место точек, в которых величина U сохраняет постоянное значение.
Это геометрическое место точек называют поверхностью уровня скалярного поля U. Ее уравнение в выбранной системе координат имеет вид: U(x,y,z) = C, где C = const.Следовательно, изменяя значения C, получаем семейство поверхностей уровня, которые заполняют всю область, где определено поле, и никакие две поверхности уровня, отвечающие различным значениям C, не имеют общих точек.
Задание всех поверхностей уровня с указанием соответствующих значений C равносильно заданию самого поля.
Указанный способ изображения поля особенно удобен, если речь идет о поле, заданном в плоской области D двух переменных. В этом случае уравнение U(x,y) = C определяет, вообще говоря, некоторую кривую линию, называемую линией уровня плоского скалярного поля.
Такие линии различных скалярных полей всем хорошо известны: линии равных высот (горизонтали) удобны для изображения размера местности, линии равных температур (изотермы) или линии равных давлений (изобары) в метеорологии и т. д.
| |
В математическом анализе, производная по направлению — это обобщение понятия производной на случай функции нескольких переменных. Производная по направлению показывает, насколько быстро функция изменяется при движении вдоль заданного направления.
Производная функции одной переменной показывает, как изменяется её значение при малом изменении аргумента. Если мы попытаемся по аналогии определить производную функции многих переменных, то столкнёмся с трудностью: в этом случае изменение аргумента (то есть точки в пространстве) может происходить в разных направлениях, и при этом будут получаться разные значения производной. Именно это соображение и приводит к определению производной по направлению.
Рассмотрим функцию  от
от  аргументов в окрестности точки
аргументов в окрестности точки  . Для любого единичного вектора
. Для любого единичного вектора  определим производную функции
определим производную функции  в точке
в точке  по направлению
по направлению  следующим образом:
следующим образом:
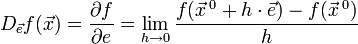
Значение этого выражения показывает, как быстро меняется значение функции при сдвиге аргумента в направлении вектора  .
.
Если направление сонаправленно с координатной осью, то производная по направлению совпадает с частной производной по этой координате.

 есть полный дифференциал функции
есть полный дифференциал функции  . В соответствии с доказательствами условий независимости криволинейного интеграла
. В соответствии с доказательствами условий независимости криволинейного интеграла  от выбора пути
от выбора пути  можно заключить, что большое количество функций, которые удовлетворяют условию
можно заключить, что большое количество функций, которые удовлетворяют условию 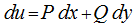 представляют собой
представляют собой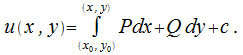
 , здесь
, здесь  и
и  представлены в качестве отрезков, которые являются параллельными осям координат (рис. 26.7). В этом случае
представлены в качестве отрезков, которые являются параллельными осям координат (рис. 26.7). В этом случае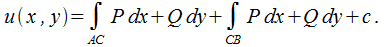
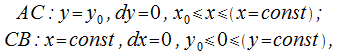
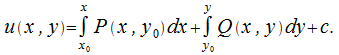
 полным дифференциалом
полным дифференциалом  Если это так, то вычислить
Если это так, то вычислить 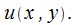
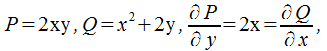
 В соответствии с (26.5) запишем
В соответствии с (26.5) запишем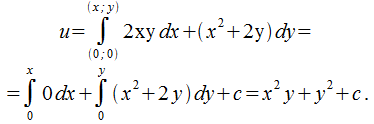
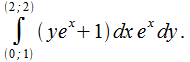
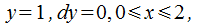

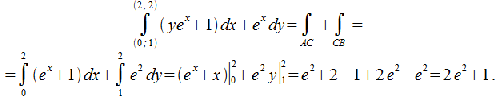


 от
от  аргументов в окрестности точки
аргументов в окрестности точки  . Для любого единичного вектора
. Для любого единичного вектора  определим производную функции
определим производную функции  в точке
в точке  по направлению
по направлению  следующим образом:
следующим образом: