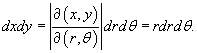Определение двойного интеграла

Понятие интеграла может быть расширено на функции двух и большего числа переменных. Рассмотрим, например, функцию двух переменных z = f (x,y). Двойной интеграл от функции f (x,y) обозначается как

где R - область интегрирования в плоскости O xy. Если определенный интеграл от функции одной переменной выражает площадь под кривой f (x) в интервале от x = a до x = b, то двойной интеграл выражает объем под поверхностью z = f (x,y) выше плоскости O xy в области интегрирования R

Двойные интегралы в полярных координатах

 

Одним из частных случаев замены переменных является переход из декартовой в полярную систему координат (оооооооооо)

кобиан такого преобразования имеет вид

Следовательно, дифференциальный элемент в полярных координатах будет равен

Пусть область интегрирования R в полярных координатах определяется следующим образом (рисунок 2):

Тогда двойной интеграл в полярных координатах описывается формулой

 

Вычисление двойного интеграла в декартовой системе координат для правильной области

Пусть область D - правильная в отношении оси Ох (рис. 2.6.)

Тогда в этом случае область D может быть задана одной системой неравенств:

Если существует двойной интеграл

(это возможно, например, если f(x; y) непрерывна на D), то его можно вычислить через повторный кратный интеграл так:

При этом внутренний интеграл по у находится при постоянном х.

Данное представление (2.11) получается из определения двойного интеграла при специальном способе разбиения области D на n "мелких" частей (линиями, параллельными либо Ох, либо Оу - прямоугольной "шахматной" сеткой. А затем выполняется суммирование "объёмов" Δ V_i сначала по оси Оу, а затем по оси Ох).