Транспортная задача. 1. Математическая постановка задачи
1. Математическая постановка задачи. Общая постановка транспортной задачи состоит в определении оптимального плана перевозок некоторого однородного груза из m пунктов отправления A1, A2,…, Am в n пунктов назначения B1,B2,…,Bn. При этом в качестве критерия оптимальности обычно берется либо минимальная стоимость перевозок груза, либо минимальное время его доставки. Рассмотрим транспортную задачу, в качестве критерия оптимальности которой взята минимальная стоимость перевозок груза. Обозначения: 1,……, m- поставщики груза, 1, …..n-потребителей, строка (i)-поставщики столбец(j)-потребитель Составим план перевозок от поставщиков к потребителям, при котором у поставщиков будет вывезен весь груз, а потребителям будет завезено столько, сколько им нужно, при этом суммарная стоимость перевозок должна быть минимальной. Вводим переменные F =
Опр1. Матрица X с неотрицательными элементами xij называется планом перевозок. Опр2 План X *= (х ij *), i=1,…, m, j=1,….,n, при котором функция принимает свое минимальное значение, называется оптимальным планом транспортной задачи. Исходные данные транспортной задачи записываются в виде таблицы:
Если общая потребность в грузе в пунктах назначения равна запасу груза в пунктах отправления, то есть
то модель такой транспортной задачи называется закрытой. Если же указанное условие не выполняется, то модель – открытая. Теорема: Для разрешимости транспортной задачи необходимо и достаточно, чтобы выполнялось равенство: Чтобы решить открытую задачу сведем ее к предыдущей. 1)Если a>b, вводим фиктивного потребителя c потребностью: Стоимость перевозки этому потребителю Все что получает фиктивный потребитель останется на складе у поставщика. 2)Если a<b, то вводим фиктивного поставщика Все что фиктивный поставщик поставит, соответствующий потребитель не дополучит. Условие закрытости транспортной задачи a = b означает, что среди m + n уравнений системы независимыми являются только m + n – 1 уравнений, поэтому в любом базисном решении этой системы должно быть m + n - 1 базисных переменных. Поскольку свободные переменные в таком решении равны нулю, то в транспортной таблице им будут соответствовать пустые клетки. · Клетки таблицы, в которые записаны отличные от нуля перевозки, называются занятыми, а остальные (пустые) - свободными. · План называется вырожденным, если количество занятых клеток в нем меньше, чем n + m -1. План называется невырожденным, если количество занятых клеток равно в точности n + m – 1 Если на каком-то этапе решения получился вырожденный план, то его необходимо пополнить, проставив в недостающем числе клеток нулевую перевозку и превратив, тем самым, эти клетки в занятые. · Циклом в транспортной таблице называется несколько клеток, соединенных замкнутой ломаной линией так, чтобы две соседние вершины ломаной были расположены либо в одной строке, либо в одном столбце. План называется ациклическим, если его занятые клетки не содержат циклов. В опорном плане не может быть циклов. Оптимальные планы являются ациклическими, поэтому и первоначальный план также должен удовлетворять этому требованию. Планы, полученные с помощью метода северо-западного угла и метода наименьшей стоимости, ациклические. Схема решения: 1)найти начальный опорный план. 2)проверить план на оптимальность. 3)если план не оптимальный, то перейти к новому опорному плану (результат не хуже предыдущего). Методы для определения опорного плана: 1. Метод северо-западного угла 2.Метод минимального элемента (3. Метод Фогеля)-можно видимо не писать раз про него нам не рассказывали
|

 - запас этого груза на складе,
- запас этого груза на складе, - размер потребления груза,
- размер потребления груза, 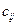 - стоимость перевозки 1 единицы груза от
- стоимость перевозки 1 единицы груза от  -го поставщика к
-го поставщика к  -му потребителю.
-му потребителю.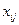 - количество единиц груза, перевозимого от i -ого поставщика к
- количество единиц груза, перевозимого от i -ого поставщика к  ,
, 
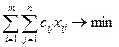 , где сij – матрицей стоимостей перевозок
, где сij – матрицей стоимостей перевозок 





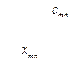
 - общее наличие груза у поставщиков,
- общее наличие груза у поставщиков,  - общая потребность в грузе
- общая потребность в грузе
 .
. .
. , сm+1j=0, j=
, сm+1j=0, j= 



