Задачи, сводящиеся к задачам линейного программирования
a. О наилучшем использовании ресурсов (Оптимизация плана производства) Необходимо определить план производства одного или нескольких видов продукции, который обеспечивает наиболее рациональное использование имеющихся материальных, финансовых и других видов ресурсов. Обозначения: n - количество выпускаемых продуктов;
- объем выпуска j -го продукта
(2) – система ограничений на объем имеющихся ресурсов; (3) – ограничения на неотрицательность переменных.
Линейная функция (3), максимум которой требуется определить, вместе с системой неравенств (2) и условием неотрицательности переменных (1) образуют математическую модель исходной задачи.
b. Задача о смесях (Оптимальное смешение) Необходимо определить наилучший способ смешения исходных ингредиентов для получения смеси с заданными свойствами и с наименьшими затратами. Обозначения: n - количество исходных ингредиентов;
- количество j -го ингредиента, входящего в смесь;
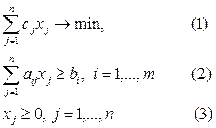
c. Задача о раскрое (Минимизация обрезков) Данная задача состоит таких технологических планов раскроя, при которых получается необходимый комплекс заготовок, а отходы (по длине, площади, объёму, массе или стоимости) сводятся к минимуму. Например, продукция бумажной фирмы выпускается в виде бумажных рулонов стандартной ширины Обозначим через В качестве переменных следует идентифицировать количество стандартных рулонов, которые должны быть разрезаны при j-м варианте раскроя. Определим переменную следующим образом: Целевая функция – минимум отходов при раскрое
Ограничение на удовлетворение спроса потребителя
|

 m - количество используемых производственных ресурсов (например, производственные мощности, сырье, рабочая сила);
m - количество используемых производственных ресурсов (например, производственные мощности, сырье, рабочая сила);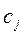 - объем затрат i -го ресурса на выпуск единицы j -й продукции;
- объем затрат i -го ресурса на выпуск единицы j -й продукции; - прибыль от выпуска и реализации единицы j -го продукта;
- прибыль от выпуска и реализации единицы j -го продукта; - количество имеющегося i -го ресурса;
- количество имеющегося i -го ресурса; (1) – целевая функция (максимум прибыли);
(1) – целевая функция (максимум прибыли); - количество i -го компонента в j -м ингредиенте;
- количество i -го компонента в j -м ингредиенте; - стоимость единицы j -го ингредиента
- стоимость единицы j -го ингредиента . По специальным заказам потребителей фирма поставляет рулоны других размеров, для этого производится разрезание стандартных рулонов. Типичные заказы на рулоны нестандартных размеров могут включать
. По специальным заказам потребителей фирма поставляет рулоны других размеров, для этого производится разрезание стандартных рулонов. Типичные заказы на рулоны нестандартных размеров могут включать  видов шириной
видов шириной  . Известна потребность в нестандартных каждого вида, она равна
. Известна потребность в нестандартных каждого вида, она равна  . Возможны
. Возможны  различных вариантов построения технологической карты раскроя рулонов стандартной ширины
различных вариантов построения технологической карты раскроя рулонов стандартной ширины 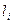 .
. количество рулонов i-го вида, получаемых при раскрое единицы стандартного рулона по j-му варианту. При каждом варианте раскроя на каждый стандартный рулон возможны потери, равные
количество рулонов i-го вида, получаемых при раскрое единицы стандартного рулона по j-му варианту. При каждом варианте раскроя на каждый стандартный рулон возможны потери, равные  . К потерям следует относить также избыточные рулоны нестандартной длинны
. К потерям следует относить также избыточные рулоны нестандартной длинны  ,
,  .
. – количество стандартных рулонов, разрезаемых по варианту
– количество стандартных рулонов, разрезаемых по варианту  ,
,  (3.29)
(3.29) ,
,  ,
,  . (3.30)
. (3.30)


