Метод потенциалов
Теорема. Если план 1) 2) для свободных клеток I шаг (вычисление потенциалов). II шаг (проверка плана на оптимальность). Если же хоть одна оценка отрицательна – то план не оптимальный. Отрицательные оценки III шаг (улучшение плана). В цикле можно шагать только по горизонтали и вертикали, шаги чередуются. Можно перешагивать через любое количество как занятых так и не занятых клеток, при этом в каждом столбце и строке не более 2-х клеток, участвующий в цикле. Примеры циклов:
Если имеем опорный план, то для каждой свободной клетки можно образовать единственный цикл, одной из вершин которого является данная клетка, а остальными являются занятые.
Среди клеток с отрицательной оценкой ищется наибольшая по модулю. Затем для этой клетки строим единственный цикл. Набор клеток в цикле помечаем поочередно знаками «+» и «–», начиная с «+» в свободной клетке, где отриц. оценка наибольшая по модулю. Среди клеток с «-» ищем минимальную поставку, обозначим эту величину за Δ Строим новый план по правилу:
Так как после пересчета у нас добавилась лишняя занятая клетка, то их количество необходимо сократить, убрав нуль в одной из клеток цикла. Если таких клеток получилось несколько, то свободной делаем ту из них, в которой тариф перевозок максимален. После этого полученный план проверяется на оптимальность описанным выше способом. Перераспределение груза производится до тех пор, пока очередной план не станет оптимальным. На этом действие алгоритма завершается.
|

 является оптимальным в транспортной задаче, то существует система из
является оптимальным в транспортной задаче, то существует система из 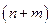 чисел
чисел  ,
,  , называемых потенциалами(
, называемых потенциалами( - потенциалы поставщиков,
- потенциалы поставщиков,  - потенциалы потребителей), удовлетворяющих следующим условиям:
- потенциалы потребителей), удовлетворяющих следующим условиям: ,-для занятых клеток
,-для занятых клеток .(Sij = cij - (u i+ vj)
.(Sij = cij - (u i+ vj)  )
)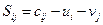 . Для занятых клеток Sij=0. Если для свободных клеток выполняется условие Sij = cij - (u i+ vj)
. Для занятых клеток Sij=0. Если для свободных клеток выполняется условие Sij = cij - (u i+ vj)  показывают, насколько возрастет целевая функция, если в эту клетку сделать поставку, равную 1.
показывают, насколько возрастет целевая функция, если в эту клетку сделать поставку, равную 1.




