Основные определения из теории графов
Ориентированным конечным графом называется пара множеств Ориентация дуги необходима, например, для изображения работы, так как она имеет начало и конец. Если ориентации нет или ее можно не учитывать, то говорят, что пара вершин соединена ребром (на рисунке изображается без стрелки). Так, если вершины графа есть станции АТС в городе, то телефонный кабель между двумя станциями можно представить ребром. Ребро ориентированного графа называется дугой. Сеть – ориентированный граф, в котором есть одна вершина - источник и одна вершина – сток. Остов графа – минимальное количество ребер, необходимое для того чтобы между каждыми 2 вершинами существовала цепь (подграф данного графа, содержащий все его вершины и являющийся деревом). Алгоритм нахождения остова - 1) выписываются ребра в порядке возрастания весов; 2) задаются 2 множества: N – множество непомеченных дуг (изначально содержит все дуги), M – множество помеченных дуг (изначально Ø); 3) Граф называется неориентированным, если его вершины соединяются только ребрами. Граф называется смешанным, если его вершины соединяются и ребрами и дугами. Далее, если не оговорено особо, Путь - это конечная последовательность дуг, в которой начало каждой следующей дуги совпадает с концом предыдущей. Замкнутый путь называется контуром. В неориентированном графе путь называется цепью, а контур - циклом. Обозначим Граф Граф Говорят, что граф Утверждение 1. Всякий граф Если дугам ориентированного графа не приписаны веса, то длина пути есть количество дуг в этом пути. Дуги вида Говорят, что вершина 1) асимметричность: из 2) транзитивность: из 3) иррефлексивность: любая вершина Иррефлексивное, транзитивное, а потому и асимметричное бинарное отношение Полный путь - путь из исходной вершины в завершающую. Полный путь называется критическим, если сумма времен выполнения работ в него входящих самая большая среди таких же времен всех других полных путей. Пропускная способность пути – минимальная из пропускных способностей дуг, в него входящих Разрез – разбиение множества вершин V ориентированного графа на 2 непересекающихся подмножества База дуг разреза – множество дуг, у которых начало лежит в множестве М, а конец в множестве N Пропускная способность базы дуг разреза – сумма пропускных способностей дуг, в нее входящих
|

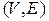 , где
, где  - множество вершин, а
- множество вершин, а  - множество дуг, каждая из которых соединяет некоторую пару вершин графа. Дуга обозначается также парой вершин, которые она соединяет, например
- множество дуг, каждая из которых соединяет некоторую пару вершин графа. Дуга обозначается также парой вершин, которые она соединяет, например  .
. - ориентированный конечный граф.
- ориентированный конечный граф. - граф, который получается из
- граф, который получается из  следует, что обратной дуги нет, то есть
следует, что обратной дуги нет, то есть  .
. называются предшествующими дуге
называются предшествующими дуге  .
.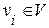 предшествует вершине
предшествует вершине  (краткая запись
(краткая запись  ), если существует путь ненулевой длины от
), если существует путь ненулевой длины от 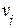 к
к  . Отношение
. Отношение 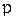 обладает следующими свойствами:
обладает следующими свойствами: ;
; следует, что
следует, что  ;
;


