Расчетные схемы балки (полоса шириной 1 см).
Общая схема.
М
В общем случае «балка» испытывает изгиб, растяжение, срез от поперечной силы. Напряжения в настиле от изгиба тем значительнее, чем он толще, чем больше δн, или меньше соотношение: ℓ н / δн Напряжения от растяжения силой «Н» тем больше, чем настил тоньше, чем он ближе к мембране, или «полоска» ближе к гибкой нити, т.е. чем больше соотношение - ℓ н / δн .
2.6. Категории стального листового настила по расчётной схеме. 1. ℓ н / δн ≤ 50 – толстый настил, растягивающие напряжения от «Н» - незначительны, ими можно пренебречь, учитывают только влияние изгиба («М»), это следствие большой нагрузки «q» (глубинные затворы, большая поперечная нагрузка). 2. ℓ н / δн > 300 – тонкий настил, изгиб влияет незначительно, расчет ведут только на действие осевой силы «Н» - настил только растянут (в перекрытиях встре- чаются очень редко - мембраны)
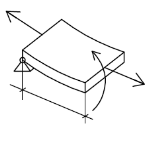
3. 50 < ℓ н / δн < 300 – настил средней толщины, занимает промежуточное положение между расчетными схемами 1-2, балка – мембрана. Учитывается изгиб + центральное растяжение (наиболее распространённый вид настила), 2.7. Расчётные схемы настилов разной толщины. 1.«толстый» настил. В местах крепления настила к балкам настила в стальном листе образуется пластические шарниры, поэтому с некоторым запасом опоры можно рассматривать как шарниры.
δн х
Основные расчётные зависимости МХMAX = 2 - е. Предельное состояние. qн
fmax
Введем понятие цилиндрической жесткости, которая учитывает влияние соседних «полосок» на «расчетную».
тот же «толстый» настил, но концы защемлены
qℓ2/12 = Mmax
qℓ2/24
2.8.Настил средней толщины (изгиб+растяжение)
Н Н
fo прочность (несущая способность) обеспечена. х у ℓ н Уравнение упругой линии в дифференциальной форме:
H H`
См х
Н Мх х
С.П. Тимошенко предложил «инженерную» формулу для упругой линии балки (растяжение+ изгиб). При малых прогибах упругую линию можно описать синусоидой вида:
здесь f0 – наибольший прогиб балки в середине, зависящий только от « q»,
Nкр =
ℓн
В данной задаче нас интересует только наибольший прогиб в середине балки при х =
Момент инерции полоски настила шириной 1 см
тогда основная формула принимает вид:
*
Основной критерий по жесткости для настила:
к
предельная длина настила
, где, qн =
Все приведенные зависимости относятся к полоске настила, шириной 1 см.
Последовательность расчёта настила
1) вычисляем полную нормативную линейную нагрузку qн ; 2) в зависимости от величины qн по таблице П.2.1.Приложения принимаем 3) окончательно принимаем
2.9. Расчет сварного шва.
Величина растягивающего осевого усилия “Н” при расчетесварного шва, крепящего настил к балке настила:
кг/см
при А = 150, Е1 = 2,3
Н = 302 / δн, где Н – кг/см; δн – см.
сварка полуавтоматическая в среде защитного газа СО2 сварочная проволока Св 0,8 Г2С. Rfw = 1850 кг/см2 , βf = 0,7 Условие не предельности.
требуемый катет Н ≤ βf ∙kf ∙Rfw; сварного шва.
kf < δн
|




 1 -е предельное состояние.
1 -е предельное состояние.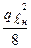 ; WХ =
; WХ =  ; WХТРЕБ =
; WХТРЕБ =  ; δн ТРЕБ =
; δн ТРЕБ =  = 0,87
= 0,87  ;
;
 пр
пр
 = 2,1
= 2,1  6
6  , D-цилиндрическая жесткость кгсм2,
, D-цилиндрическая жесткость кгсм2, пр
пр


 пр
пр




 Расчетная схема fmax
Расчетная схема fmax  <
<  < 300 решающим является расчет на жесткость.
< 300 решающим является расчет на жесткость. Если выполняется условие по жесткости, то
Если выполняется условие по жесткости, то - нормативная нагрузка.
- нормативная нагрузка.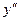 = Mx = M0 - H
= Mx = M0 - H 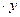
 Н
Н sin
sin 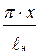
 - наибольший балочный прогиб,
- наибольший балочный прогиб,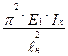 - критическая «Эйлерова» сила для гибкого стержня.
- критическая «Эйлерова» сила для гибкого стержня.


 .
.








 х 1 см δн
х 1 см δн 
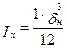 ;
;
 пр =
пр =  ; где А = 150 (требование СНиП)
; где А = 150 (требование СНиП) ; подставив значение I X и fmax в выражение *, получим:
; подставив значение I X и fmax в выражение *, получим: пр =
пр = 
 *,*, тогда
*,*, тогда пр, при которой прогиб достигает предельно допустимой величины:
пр, при которой прогиб достигает предельно допустимой величины:
 пр =
пр =  н
н
 ,
, , qн =
, qн = 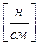 .
. н и по *** находим
н и по *** находим  пр;
пр;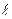 н так, чтобы
н так, чтобы 



 - обычно получается небольшим; поэтому принимаем конструктивно kf ≥ 4 мм
- обычно получается небольшим; поэтому принимаем конструктивно kf ≥ 4 мм


