Решение. 1. Решим первое неравенство системы:
1. Решим первое неравенство системы:
Пусть
Решение первого неравенства исходной системы
2. Решим второе неравенство системы:
Решение второго неравенства системы:
3. Поскольку
Ответ: 3. C 3. Решите систему неравенств
Решение. Рассмотрим уравнение
Для решения второго неравенства используем следующие теоремы о знаках: при положительных
Тогда имеем:
Методом интервалов найдем решения: Поскольку
Ответ: 4. C 3. Решите систему неравенств
Решение. Рассмотрим первое неравенство системы. Положим
Рассмотрим второе неравенство системы. Так как
Сравним числа Ответ: 5. C 3. Решите систему неравенств
Вариант № 3774478 1. C 3. Решите систему неравенств
|


 тогда неравенство примет вид:
тогда неравенство примет вид:  откуда
откуда


 где
где  где
где 

 получаем решение исходной системы неравенств:
получаем решение исходной системы неравенств: 


 . По теореме, обратной теореме Виета, сумма его корней равна
. По теореме, обратной теореме Виета, сумма его корней равна  , а их произведение равно
, а их произведение равно  . Поэтому это числа
. Поэтому это числа  и
и 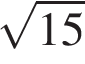 . Тогда для первого неравенства системы имеем:
. Тогда для первого неравенства системы имеем:
 выражения
выражения  и
и  имеют одинаковые знаки; для любых для
имеют одинаковые знаки; для любых для  выражения
выражения  и
и  имеют одинаковые знаки.
имеют одинаковые знаки.

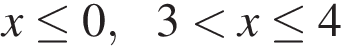 или
или 
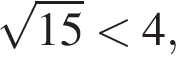 получаем решение системы.
получаем решение системы.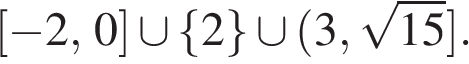

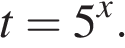 Тогда неравенство принимает вид
Тогда неравенство принимает вид  откуда
откуда  Таким образом,
Таким образом, 
 и
и  для любого
для любого  воспользовавшись тождеством
воспользовавшись тождеством  и методом интервалов, получаем:
и методом интервалов, получаем:


 и
и 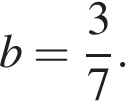 Имеем
Имеем  а, значит,
а, значит,  т. е.,
т. е.,  откуда и получаем решение данной системы
откуда и получаем решение данной системы 





