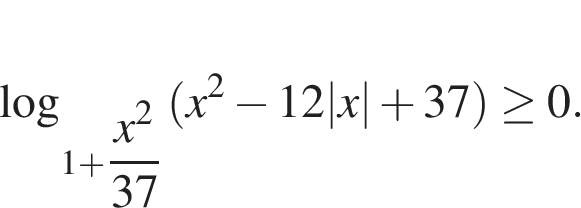Решение. Поскольку призма прямая, то высота треугольника перпендикулярна плоскости
Поскольку призма
Так как
Отсюда
Ответ: 5. C 2. В правильную шестиугольную пирамиду, боковое ребро которой равно
Вариант № 3761272 1. C 3. Решите систему
Решение. Решим первое неравенство
2. Решим второе неравенство:
3. Решением системы является общая часть решений двух неравенств. Поскольку
Ответ: 2.C 3. Решите систему неравенств:
Решение. Решим первое неравенство. Сделаем замену
Обратная замена дает Решим второе неравенство. Заметим, что
поэтому неравенство
Таким образом, получаем:
Ответ: 3. C 3. Решите систему неравенств
Решение. Решим первое неравенство:
Осталось найти положительные решения второго неравенства. Заметим, что выражение, стоящее под знаком логарифма, не меньше 1:
При положительных значениях переменной справедливы неравенства
Тем самым, неравенство выполнено в том и только В том случае, когда оба выражения равны нулю. Следовательно,
Отрицательное решение неравенства не является решением системы. Ответ: 4. C 3. Решите систему неравенств
|

 прямая, то высота
прямая, то высота  треугольника
треугольника  перпендикулярна плоскости
перпендикулярна плоскости  Поэтому прямая
Поэтому прямая  — проекция прямой
— проекция прямой  на плоскость
на плоскость 

 имеем:
имеем: 

 Следовательно,
Следовательно, 



 , а высота равна 1, вписана сфера. (Сфера касается всех граней пирамиды.) Найдите площадь этой сферы.
, а высота равна 1, вписана сфера. (Сфера касается всех граней пирамиды.) Найдите площадь этой сферы.



 , получаем.
, получаем. .
.
 получаем
получаем или
или 
 или
или 

 выполнено при всех
выполнено при всех  , кроме всех
, кроме всех  и
и  причем
причем и
и 


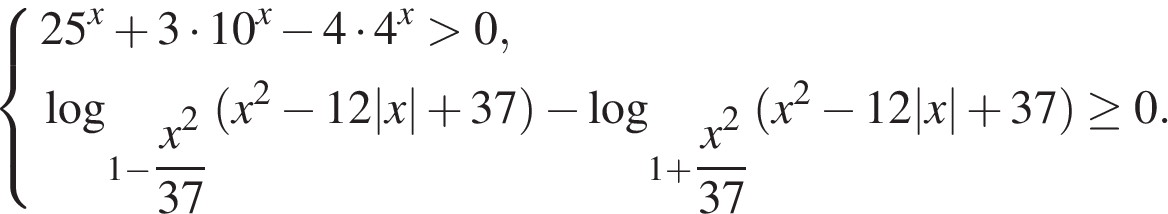


 и
и  а значит,
а значит, и
и