УСЛОВНЫЙ ОПЕРАТОР IF
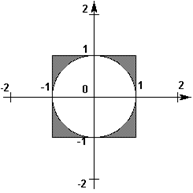
Цель работы: формирование знаний и умений по работе с операторами языка. Научиться решать задачи на разветвляющиеся алгоритмы.Приобретение навыков написания программ с использованием условного оператора IF. 1. Построить программу, которая вводит координаты точки (x, y) и определяет, попадает ли точка в заштрихованную область на рисунке. Попадание на границу области считать попаданием в область. 2. Определить, лежит ли точка с координатами (x 1, y 1) внутри прямоугольника, ограниченного прямыми x = a, x = b, y = c, y = d. 3. Написать программу, которая печатает True или False в зависимости от того, выполняются или нет заданные условия: o квадрат заданного трехзначного числа равен кубу суммы цифр этого числа; o сумма двух первых цифр заданного четырехзначного числа равна сумме двух его последних цифр; 4. Написать программу, определяющую по длинам сторон треугольника, является ли он прямоугольным. Если треугольник не прямоугольный, то вычислить косинус угла, лежащего против большей стороны. 5. Даны действительные числа x, y. Если x, y отрицательны, то каждое значение заменить его модулем; если отрицательное только одно из них, то оба значения увеличить на 0.5; если оба значения не отрицательны и ни одно из них не принадлежит отрезку [0.5, 2.0], то оба значения уменьшить в 10 раз; в остальных случаях x, y оставить без изменения. 6. Построить программу, которая вводит координаты точки (x, y) и определяет, попадает ли точка в заштрихованную область на рисунке. Попадание на границу области считать попаданием в область. 7. Определить, лежит ли точка с координатами (x, y) внутри сектора окружности с радиусом r и центром в точке (xc; yc). Стороны сектора параллельны осям координат. 8. Даны три точки А (x1, y1), B(x2, y2), C(x3, y3). Определить, будут ли они расположены на одной прямой. Если нет, то вычислить периметр треугольника ABC. 9. Построить программу, которая вводит координаты точки (x, y) и определяет, попадает ли точка в заштрихованную область на рисунке. Попадание на границу области считать попаданием в область. 10. Вычислить значение функции y по одной из следующих формул: y = x 2+3, если x <0; y =(x 2+3), если 0£ x <1; y = x (x 2+3), если x ³1. 11. Написать программу, определяющую, будут ли прямые А1х + В1у + С = 0 и А2х + В2у + С = 0 перпендикулярны. Если нет, то найти угол между ними. 12. На оси ОХ расположены три точки а, b, с. Определить, какая из точек b,c расположена ближе к а. 13. Определить, лежит ли точка с координатами (x, y) внутри кольца с радиусами r 1, r 2и центром в точке (xc; yc). 14. Два прямоугольника, расположенные в первом квадранте, со сторонами, параллельными осям координат, заданы координатами своих левого верхнего и правого нижнего углов. Для первого прямоугольника это точки (x1, y1) и(x2, 0),для второго — (x3, y3), (x4, 0) Составить программу, определяющую, пересекаются ли данные прямоугольники, и вычисляющую площадь общей части, если они пересекаются. 15. Вычислить значение функции: ì x 3+ y 3,если x > y
F (x, y) = í x 2- y2,если x и y –нечетные î0,иначе 16. Даны действительные числа a, b, c, x, y. Выяснить, пройдет ли кирпич с ребрами a,b,c в прямоугольное отверстие со сторонами x и y. Просовывать кирпич в отверстие разрешается только так, чтобы каждое из его ребер было параллельно или перпендикулярно каждой из сторон отверстия. 17. Определить, лежит ли точка с координатами (x, y) внутри верхней половины кольца с радиусами r 1и r 2и центром в точке (xc; yc).
18. Вычислить значение функции, если x и y – целые: ì x 2+ y 2,если x и y -четные
F (x, y) = í x 2- y2,если x и y -нечетные î(x+y)2,иначе 19. Даны значения a, b, c. Если ни одно из значений не равно нулю, 20. Построить программу, которая вводит координаты точки (x, y) и определяет, попадает ли точка в заштрихованную область на рисунке. Попадание на границу области считать попаданием в область. 21. Вычислить значение функции y по одной из следующих формул: y = x 2–3, если x <1; y =(x 2–3)2, если 1<= x <5; y = (x 2–3)/ x, если x >=5. 22. Написать программу, которая печатает True или False в зависимости от того, выполняются или нет заданные условия: o среди цифр заданного трехзначного числа есть одинаковые; o среди первых трех цифр из дробной части заданного положительного вещественного числа есть цифра 0. 23. Определить и вывести на печать номер квадранта, в котором расположена точка М(x,y), x и y заданные вещественные числа. 24. Даны шесть монет, из которых одна фальшивая. Фальшивая монета отличается от настоящей монеты только весом, причем она либо немного тяжелее, либо немного легче. Имея рычажные весы, определить ложную монету не более чем за три взвешивания. 25. Вычислить значение функции:
î0,иначе 26. Из величин, определяемых выражениями a=sinx, b=cosx, c=ln|x| при заданном х, определить и вывести на экран дисплея минимальное значение. 27. Даны значения a, b, c. Если a > b и b > c, то вычислить x =0,2; y = x 2+0,6 x +sin(x /2), если b < c и a < c, то x =2; y = x 3+ x 2+ x +1, в остальных случаях x =0, y =0. 28. Даны три числа a, b, c. Вычислить экспоненту того числа, значение которого ближе всего к значению функции y =(a 2+ b 2+ c 2)/(a + b + c). Если a + b + c =0, то вывести сообщение об этом. 29. Даны три числа a, b, c. Определить количество отрицательных и количество положительных чисел. 30. Найти наименьшее из трех заданных значений a, b, c и вывести его имя и значение. 31. Построить программу, которая вводит координаты точки (x, y) и определяет, попадает ли точка в заштрихованную область на рисунке. Попадание на границу области считать попаданием в область. 32. Определить, какая из двух точек - M1(x1,y1) или M2(x2,y2) - расположена ближе к началу координат. Вывести на экран дисплея координаты этой точки. 33. Определить, попадает ли точка M(x,y) в круг радиусом r с центром в точке (x0,y0). 34. Дана точка А (х, у). Определить, принадлежит ли она треугольнику с вершинами в точках (x1, y1), (x2, y2), (x3, y3). 35. Построить программу, которая вводит координаты точки (x, y) и определяет, попадает ли точка в заштрихованную область на рисунке. Попадание на границу области считать попаданием в область.
|




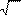 то вычислить D =1/ a +1/ b +1/ c, и если D >0 и a >0, вычислить y = D^(1/2), в противном случае y =2. Если хотя бы одно из значений a, b, c равно нулю, то вывести сообщение «Нет решения».
то вычислить D =1/ a +1/ b +1/ c, и если D >0 и a >0, вычислить y = D^(1/2), в противном случае y =2. Если хотя бы одно из значений a, b, c равно нулю, то вывести сообщение «Нет решения».