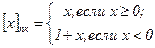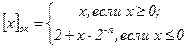Введение. В общем виде число А в p-ной позиционной системе счисления представляется в виде:
В общем виде число А в p -ной позиционной системе счисления представляется в виде:
=
При k = Const получается число с фиксированной точкой: k=0: правильная дробь – число с фиксированной запятой A = a-1*p-1+a-2*p-2+…+a-m*p-m k=r: целое число – число с фиксированной точкой A = an*pn+an-1*pn-1+…+a1*p1+a0*p0 При k ≠ Const получается число с плавающей запятой.
Данная лабораторная работа посвящена изучению чисел с фиксированной точкой. При дальнейшем описании мы будем ориентироваться на числа с фиксированной запятой в этом классе представления чисел. Однако все представленные теоретические обоснования легко экстраполировать и на числа с фиксированной точкой в строгом смысле этого термина.
Прямой код. Возможны два варианта изображения знаков чисел двоичными цифрами: «+» обозначать «0», а «-» обозначать «1»; «+» обозначать «1», а «-» обозначать «0». Оба варианта равноценны. На практике в основном используется первый вариант. При таком решении все положительные числа имеют вид: 0,..., а отрицательные: 1,.... В данном случае знаковая цифра (код знака) помещается слева от запятой на место разряда с весом 2° (рис.).
Рис. Представление числа с фиксированной запятой в прямом коде.
Если знак и цифровую часть числа рассматривать как единое целое, то изображение положительных чисел не изменяется и определяется интервалом 0 ≤ х < 1, а все отрицательные числа изображаются положительными числами [х]пк, расположенными в интервале 1 ≤ [х]пк<2. Рассмотренную связь между числом х и его изображением в прямом коде — [х]пк можно представить в виде: Таким образом, число, заданное в прямом коде, можно описать следующим образом: Хпк = ЗнХ.|X| Примеры: +510 = 0.1012пк -510 = 1.1012пк
Методика выполнения алгебраического сложения, рациональная для применения в ЭВМ, должна удовлетворять следующим условиям: • обработка знаковых и цифровых разрядов суммируемых чисел X и Y должна производиться по одинаковым правилам с получением при этом правильного знака суммы; • должна исключаться операция прямого вычитания, и вместо неё алгебраическое суммирование чисел разных знаков должно выполняться как сложение специальных кодов суммируемых чисел; • должно определяться переполнение, соответствующее
Числа, представленные в прямом коде, не соответствуют данным условиям, в частности, пункту 2. Поэтому для арифметических операций в ЭВМ прямой код представления чисел практически не используется.
Всем указанным условиям удовлетворяет методика алгебраического сложения дополнительных и обратных кодов исходных чисел.
Обратный код. В этом коде связь между числом х и его изображением в обратном коде [х]окопределяется равенством:
Покажем, как практически представить в обратном коде отрицательное число. При х ≤ 0: Xок = 2 + х – 2-n = 2 - |x| - 2-n: _10.00...00 2 00.00...01 2-n 1.11...11 2 - 2-n
_1. 1 1... 1 1 2 - 2-n 0.x1x2...xn-1xn |x| 0. x̅1x̅2...x̅n-1x̅n Таким образом, для отрицательного числа получение обратного кода заключается в присвоении знаковому разряду кода 1 и замене 0 на 1, а 1 на 0 в цифровой части модуля числа. Примеры: +510 = 0.1012пк = 0.1012ок -510 = 1.1012пк = 1.0102ок
При обратном преобразовании, о есть при переходе от обратного кода к прямому, от обратного кода берется обратный код.
|

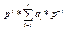 A = an*pn+an-1*pn-1+…+a1*p1+a0*p0+a-1*p-1+a-2*p-2+…+a-m*p-m =
A = an*pn+an-1*pn-1+…+a1*p1+a0*p0+a-1*p-1+a-2*p-2+…+a-m*p-m =