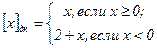Методика алгебраического суммирования в обратном коде при представлении исходных чисел и суммы в прямом коде.

Возможные комбинации, которые могут встретиться при операции сложения.

1). Х>0 и Y >0, а X + Y<1. В данном случае, обращение к обратному коду не приводит к специфике выполнения операции, так как [Х>0]_о + [ Y >0]_о = X + Y.

1a). Х>0 и Y>0, а X + Y≥1.

Эта ситуация трактуется в ЭВМ как положительное переполнение, т.к. по определению числа с фиксированной запятой его модуль должен быть строго меньше 1. В данном формате полученный результат не может быть представлен. При этом необходимо лишь зафиксировать факт появления такой ошибки. Её определение базируется на том факте, что в данном случае суммирование приводит к появлению 1 в позиции с весом 2¹, то есть в знаковом разряде результата. Обратный код не приспособлен для автоматической фиксации переполнения. Определить положительное переполнение можно по наличию 1 в знаковом разряде результата при положительных обоих слагаемых.

 

2). Х>0, Y<0 и X + Y>0.

[Х]_ок + [Y]_ок = X + 2 + Y - 2^-n – предварительный результат.

Т.к. X + Y>0, то действительный результат равен X + Y. Для того чтобы от предварительного результата перейти к действительному, необходима коррекция: вычесть 2 и прибавить 2^-n к предварительному результату, т.е. в предварительном результате исключается 1 в разряде с весом 2¹, что равноценно вычитанию 2, и эту же единицу направлить в младший разряд предварительного результата, что равноценно прибавлению 2^-n.

 

3) Х>0, Y<0 и X + Y <0.

[Х]₀ + [У]₀ = X + (2+Y - 2^-n). Этот результат соответствует правильному, так как согласно условию

X + Y<0 и [X + У<0]_о = 2 +(X + У) - 2^-n.

 

При суммировании в обратном коде чисел разных знаков возможно получение результата, равного нулю: X + Y = 0. Здесь методика суммирования обратных кодов исходных чисел не изменяется, а результат получается в виде 1,1...1. Например,

[Х]_пк = 0,1011 [Х]_ок = 0,1011

[Y]_пк = 1,1011 [Y]_ок= 1,0100

[Х + Y]₀=1,1111

Получили обратный код отрицательного нуля:

[- 0,0... 0 ]_ОК = 1,1... 1.

Такой результат согласуется с формулой, где указано, что X = 0 может иметь двоякое изображение: код положительного нуля и код отрицательного нуля. Однако в ЭВМ каждое число должно иметь однозначное представление. Поэтому при получении в качестве результата кода отрицательного нуля при выполнении операции сложения чисел в обратном коде аппаратные средства ЭВМ преобразуют его в код положительного нуля 0,0... 0, и в таком виде результат отправляется на хранение в приёмник результата.

 

4) Х<0, У<0 и |Х + У|<1.

[X]_ОК + [Y]_ок = (2 + X - 2^-n ) + (2 + Y -2^-n) - предварительный результат.

Правильный результат [(X + У)<0]_ок = 2+Х + Y - 2^-n.

Это определяет необходимость выполнения коррекции предварительного результата, которая аналогична рассмотренной в случае 2, т.е. вычесть 2 и прибавить 2^-n к предварительному результату.

4a). Х<0, Y<0, а |X + Y|≥1.

Эта ситуация трактуется в ЭВМ как отрицательное переполнение. Определить отрицательное переполнение можно по наличию 0 в знаковом разряде результата при отрицательных обоих слагаемых.

 

Дополнительный код. Здесь связь между числом X и его изображением в дополнительном коде [Х]_дк определяется равенством:

 

Сравнение данного выражение с формулой получения обратного кода показывает, что в случае отрицательного числа для получения его дополнительного кода необходимо все разряды цифровой части числа заменить на противоположные и к младшему разряду полученного результата прибавить 1.

Примеры: +5₁₀ = 0.101₂пк = 0.101₂ок= 0.101₂дк

-5₁₀ = 1.101₂пк = 1.010₂ок = 1.011₂дк

Обратное преобразование отрицательного числа (от дополнительного кода к прямому) выполняется аналогичным образом: для положительных чисел их прямой и дополнительный коды совпадают, а для получения прямого кода отрицательного числа, представленного в дополнительном коде, необходимо все разряды цифровой части числа заменить на противоположные и к младшему разряду полученного результата прибавить 1.