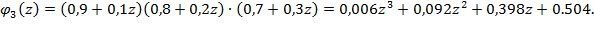Формула Бернулли
Пусть производятся п независимых испытаний, в каждом из которых может произойти некоторое событие А (по традиции такой исход опыта называют успехом) с одной и той же вероятностью Р(А) = р или произойти противоположное событие
Отсюда, в частности, следует, что вероятность того, что в п испытаниях, удовлетворяющих схеме Бернулли, событие А наступит: а ) менее m раз – равна б) более т раз — равна в) хотя бы один раз — равна г) не менее m1 раз и не более m2 раз равна
Число m0 (
Если в каждом из п независимых испытаний вероятность наступления события А равна pi (числа pi, вообще говоря, разные), то вероятность
Функция 6.1. Игральную кость подбрасывают 10 раз. Найти вероятность того, чтошестерка выпадет: О Проводится 10 независимых испытаний, Каждое испытание имеет два исхода: шестерка выпадет и шестерка не выпадет. Вероятность выпадения шестерки в каждом испытании постоянна и равна 1/6, те. р = 1/6. Таки образом, мы имеем дело со схемой Бернулли. Для нахождения искомых вероятностей применим формулу Бернулли. а)Здесь п = 10, т = 2, р = 1/6, q = 1— 1/6 = 5/6. Отсюда
б) Искомая вероятность равна
Однако в этом случае проще найти вероятность противоположного события шестерка выпадет более 8 раз, т. е. выпадет 9 или 10 раз. Имеем:
Итак, вероятность того, что шестерка выпадет не более восьми раз, равна
в)Искомая вероятность равна или 6.2. Всхожесть семян данного сорта растений составляет 70%. Найти наивероятнейшее число вcхожих семян в партии из 240 семян. О Наивероятнейшее число m0 всхожих семян находим из условия Поскольку п = 240, р = 0,7 и q = 0,3 то 6.3. Прибор состоит из 3 независимо работающих элементов. Вероятности отказов элементов за время t различны и соответственно равны: р1 = 0,1, р2 = 0,2, р3 = 0,3. Найти вероятности того, что за время t откажут: а)все элементы; б) два элемента; в) один элемент, г) ноль элементов. О Так как р1 = 0,1, р2 = 0,2, р3 = 0,3, то вероятности того, что элементы не откажут, соответственно равны: q1 = 0,9, q2 = 0,8, q3 = 0,7. Составим производящую функцию:
Отсюда следует, что: а) Р3(3) = 0,006; б) Р3(2) = 0,092; в) Р3(1) = 0,398; г) Р3(0) = 0,504. 6.4. По мишени произведено 3 выстрела. Вероятность попадания при каждом выстреле равна 0,7. Найти вероятность п попаданий в мишень, где n = 0, 1, 2, 3. 6.5. Тест содержит 10 вопросов, на которые следует отвечать, используя одно из двух слов: да, нет. Какова вероятность получения неменее 80% правильных ответов, если использовать «метод угадывания»? 6.6.Пусть вероятность того, что студент опоздает на лекцию, равна 0,08. Найти наиболее вероятное число опоздавших из 96 студентов. 6.7. В ящике находится 70% стандартных и 30% нестандартных де талей. Найти вероятность того, что из 5 взятых наудачу деталей не более одной окажется нестандартными. 6.8. Корабль выходит из строя, если получит не менее 5 попадания в надводную часть или 2 попадания в подводную часть. Найти вероятность выхода из строя корабля при 5 попаданиях, если вероятности попадания в надводную и подводную части при попадании в корабль относятся как семь к трем. 6.9. В семье 6 детей. Найти вероятность того, что в данной семье не менее двух мальчиков, но не более четырех. Считать вероятности рождения мальчика идевочки равными 0,5. 6.10. В помещении 6 электролампочек. Вероятность того, что каждая лампочка останется исправной в течение года равна 0,7. Найти: а) вероятность того что в течение года придется заменить 2 лампочки; б) наивероятнейшее число лампочек, которые будут работать в течение года.
|

 ( такойисход называют неудачей) с вероятностью Р(А) = q = 1— р (такого рода схема испытаний называется схемой Бернулли). Тогда вероятность того, что событие А наступит ровно m раз находится по формуле Бернулли:
( такойисход называют неудачей) с вероятностью Р(А) = q = 1— р (такого рода схема испытаний называется схемой Бернулли). Тогда вероятность того, что событие А наступит ровно m раз находится по формуле Бернулли: , m = 0, 1, 2, …, n.
, m = 0, 1, 2, …, n. :
: .
.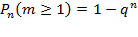 ;
;
 ) называется наивероятнейшим числом наступлений события А (или наиболее вероятным числом успехов) в схеме Бернулли, если
) называется наивероятнейшим числом наступлений события А (или наиболее вероятным числом успехов) в схеме Бернулли, если  для всех т = 0, 1, 2, …, n. Если вероятности р и q отличны отнуля, то число m0 определятся из двойного неравенства
для всех т = 0, 1, 2, …, n. Если вероятности р и q отличны отнуля, то число m0 определятся из двойного неравенства
 того, что в этойсерии испытаний событие А наступит m раз, равна коэффициенту при m -й степени (т. е. при zm) многочлена
того, что в этойсерии испытаний событие А наступит m раз, равна коэффициенту при m -й степени (т. е. при zm) многочлена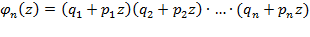
 при этом называется производящей функцией.
при этом называется производящей функцией.



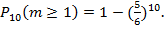 Ее можно найти и так (что, конечно, гораздо сложнее):
Ее можно найти и так (что, конечно, гораздо сложнее): 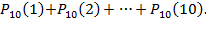

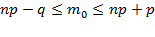 .
. т.е.
т.е.  Отсюда следует, что m0 = 168.
Отсюда следует, что m0 = 168.